implements a non-linear transient mixed-hybrid FE Darcy solver. More...

#include <DarcySolverTransientNonLinear.hpp>

Inheritance diagram for DarcySolverTransientNonLinear< MeshType >:

Collaboration diagram for DarcySolverTransientNonLinear< MeshType >:

Public Types
typedef MeshType	mesh_Type
	Typedef for mesh template. More...

typedef DarcySolverTransientNonLinear< mesh_Type >	darcySolverTransientNonLinear_Type
	Self typedef. More...

typedef DarcySolverLinear< mesh_Type >	darcySolverLinear_Type
	Darcy solver class. More...

typedef DarcySolverNonLinear< mesh_Type >	darcySolverNonLinear_Type
	Darcy non linear solver class. More...

typedef DarcySolverTransient< mesh_Type >	darcySolverTransient_Type
	Darcy transient solver class. More...

typedef darcySolverLinear_Type::data_Type	data_Type
	Typedef for the data type. More...

typedef darcySolverLinear_Type::dataPtr_Type	dataPtr_Type
	Shared pointer for the data type. More...

typedef darcySolverLinear_Type::matrixFctPtr_Type	matrixFctPtr_Type
	Shared pointer to a matrix value function. More...

typedef darcySolverLinear_Type::vector_Type	vector_Type
	Distributed vector. More...

Constructors & destructor
	DarcySolverTransientNonLinear ()
	Constructor for the class. More...

virtual	~DarcySolverTransientNonLinear ()
	Virtual destructor. More...

Methods
virtual void	setup ()
	Set up the linear solver, the preconditioner for the linear system and the exporter to save the solution. More...

virtual void	solve ()
	Solve the problem calling the non linear solver. More...

Set methods
void	setInversePermeability (const matrixFctPtr_Type &invPerm)
	Set the inverse of diffusion tensor. More...

Private Constructors
	DarcySolverTransientNonLinear (const darcySolverTransientNonLinear_Type &)
	Inhibited copy constructor. More...

Private Operators
darcySolverTransientNonLinear_Type &	operator= (const darcySolverTransientNonLinear_Type &)
	Inhibited assign operator. More...

Protected Methods
virtual void	resetVariables ()
	Update all problem variables. More...

virtual void	localMatrixComputation (const UInt &iElem, MatrixElemental &elmatMix, MatrixElemental &elmatReactionTerm)
	Compute elementary matrices. More...

virtual void	localVectorComputation (const UInt &iElem, VectorElemental &elvecMix)
	Computes local vectors. More...

Additional Inherited Members
Public Types inherited from DarcySolverNonLinear< MeshType >
typedef MeshType	mesh_Type
	Typedef for mesh template. More...

typedef DarcySolverNonLinear< mesh_Type >	darcySolverNonLinear_Type
	Self typedef. More...

typedef DarcySolverLinear< mesh_Type >	darcySolverLinear_Type
	Darcy solver class. More...

typedef darcySolverLinear_Type::data_Type	data_Type
	Typedef for the data type. More...

typedef darcySolverLinear_Type::dataPtr_Type	dataPtr_Type
	Shared pointer for the data type. More...

typedef darcySolverLinear_Type::scalarFctPtr_Type	scalarFctPtr_Type
	Shared pointer to a scalar value function. More...

typedef darcySolverLinear_Type::matrixFctPtr_Type	matrixFctPtr_Type
	Shared pointer to a matrix value function. More...

typedef darcySolverLinear_Type::scalarField_Type	scalarField_Type
	Scalar field. More...

typedef darcySolverLinear_Type::scalarFieldPtr_Type	scalarFieldPtr_Type
	Shared pointer to a scalar field. More...

Public Types inherited from DarcySolverLinear< MeshType >
typedef MeshType	mesh_Type
	Typedef for mesh template. More...

typedef LinearSolver	solver_Type
	Typedef for solver template. More...

typedef DarcySolverLinear< mesh_Type >	darcySolver_Type
	Self typedef. More...

typedef DarcyData< mesh_Type >	data_Type
	Typedef for the data type. More...

typedef std::shared_ptr< data_Type >	dataPtr_Type
	Shared pointer for the data type. More...

typedef BCHandler	bcHandler_Type
	Boundary condition handler. More...

typedef std::shared_ptr< bcHandler_Type >	bcHandlerPtr_Type
	Shared pointer to a boundary condition handler. More...

typedef std::shared_ptr< Epetra_Comm >	commPtr_Type
	Shared pointer to a MPI communicator. More...

typedef MapEpetra	map_Type
	Map type. More...

typedef std::shared_ptr< Displayer >	displayerPtr_Type
	Shared pointer to a displayer. More...

typedef FESpace< mesh_Type, map_Type >	fESpace_Type
	Finite element space. More...

typedef std::shared_ptr< fESpace_Type >	fESpacePtr_Type
	Shared pointer to a finite element space. More...

typedef FEScalarField< mesh_Type, map_Type >	scalarField_Type
	Scalar field. More...

typedef std::shared_ptr< scalarField_Type >	scalarFieldPtr_Type
	Shared pointer to a scalar field. More...

typedef FEVectorField< mesh_Type, map_Type >	vectorField_Type
	Vector field. More...

typedef std::shared_ptr< vectorField_Type >	vectorFieldPtr_Type
	Shared pointer to a scalar field. More...

typedef FEFunction< mesh_Type, map_Type, Real >	scalarFct_Type
	Scalar value function. More...

typedef std::shared_ptr< scalarFct_Type >	scalarFctPtr_Type
	Shared pointer to a scalar value function. More...

typedef FEFunction< mesh_Type, map_Type, Vector >	vectorFct_Type
	Vector value function. More...

typedef std::shared_ptr< vectorFct_Type >	vectorFctPtr_Type
	Shared pointer to a vector value function. More...

typedef FEFunction< mesh_Type, map_Type, Matrix >	matrixFct_Type
	Matrix value funcion. More...

typedef std::shared_ptr< matrixFct_Type >	matrixFctPtr_Type
	Shared pointer to a matrix value function. More...

typedef solver_Type::matrix_Type	matrix_Type
	Sparse and distributed matrix. More...

typedef solver_Type::matrixPtr_Type	matrixPtr_Type
	Shared pointer to a sparse and distributed matrix. More...

typedef solver_Type::vector_Type	vector_Type
	Distributed vector. More...

typedef solver_Type::vectorPtr_Type	vectorPtr_Type
	Shared pointer to a distributed vector. More...

typedef solver_Type::preconditionerPtr_Type	preconditionerPtr_Type
	Shared pointer to the preconditioner. More...

Public Types inherited from DarcySolverTransient< MeshType >
typedef MeshType	mesh_Type
	Typedef for mesh template. More...

typedef DarcySolverTransient< mesh_Type >	darcySolverTransient_Type
	Self typedef. More...

typedef DarcySolverLinear< mesh_Type >	darcySolverLinear_Type
	Darcy solver class. More...

typedef darcySolverLinear_Type::data_Type	data_Type
	Typedef for the data type. More...

typedef darcySolverLinear_Type::dataPtr_Type	dataPtr_Type
	Shared pointer for the data type. More...

typedef darcySolverLinear_Type::scalarFctPtr_Type	scalarFctPtr_Type
	Shared pointer to a scalar value function. More...

typedef darcySolverLinear_Type::vectorPtr_Type	vectorPtr_Type
	Shared pointer to a distributed vector. More...

typedef darcySolverLinear_Type::vector_Type	vector_Type
	Distributed vector. More...

typedef darcySolverLinear_Type::scalarFieldPtr_Type	scalarFieldPtr_Type
	Shared pointer to a scalar field. More...

typedef darcySolverLinear_Type::scalarField_Type	scalarField_Type
	Scalar field. More...

typedef std::vector< MatrixElemental >	matrixElementalContainer_Type
	Container of matrix elemental. More...

typedef TimeAdvanceBDF< vector_Type >	timeAdvance_Type
	Time advance scheme. More...

typedef std::shared_ptr< timeAdvance_Type >	timeAdvancePtr_Type
	Shared pointer to a time advance scheme. More...

Public Member Functions inherited from DarcySolverNonLinear< MeshType >
	DarcySolverNonLinear ()
	Constructor for the class. More...

virtual	~DarcySolverNonLinear ()
	Virtual destructor. More...

void	setPrimalZeroIteration (const scalarFctPtr_Type &primalZeroIteration)
	Initial guess for fixed point iteration. More...

void	setFixedPointTolerance (const Real &tol)

void	setFixedPointMaxIteration (const UInt &maxit)

UInt	fixedPointNumIteration ()

Real	fixedPointResidual ()
	Returns the residual between two iterations of the fixed point scheme. More...

const Real &	fixedPointTolerance () const
	Returns fixed point tolerance. More...

Real &	fixedPointTolerance ()
	Returns fixed point tolerance. More...

const UInt &	fixedPointMaxIteration () const
	Returns maximum number of fixed point iterations allowed. More...

UInt &	fixedPointMaxIteration ()
	Returns maximum number of fixed point iterations allowed. More...

const scalarFieldPtr_Type &	primalPreviousIterationPtr () const
	Returns the pointer of the primal solution field at previous step. More...

scalarFieldPtr_Type &	primalPreviousIterationPtr ()
	Returns the pointer of the primal solution field at previous step. More...

Public Member Functions inherited from DarcySolverLinear< MeshType >
	DarcySolverLinear ()
	Constructor for the class. More...

virtual	~DarcySolverLinear ()
	Virtual destructor. More...

void	buildSystem ()
	Build the global hybrid system, the right hand and apply the boundary conditions. More...

void	solveLinearSystem ()
	Solve the global hybrid system. More...

void	computePrimalAndDual ()
	Compute primal and dual variables from the hybrid variable as a post process. More...

void	setData (dataPtr_Type &data)
	Set the data. More...

void	setBoundaryConditions (bcHandlerPtr_Type &bcHandler)
	Set the boundary conditions. More...

void	setScalarSource (const scalarFctPtr_Type &scalarSourceFct)
	Set scalar source term. More...

void	setVectorSource (const vectorFctPtr_Type &vectorSourceFct)
	Set vector source term. More...

void	setReactionTerm (const scalarFctPtr_Type &reactionTermFct)
	Set the coefficient for the reaction term. More...

void	setHybridField (const scalarFieldPtr_Type &hybridField)
	Set the hybrid field vector. More...

void	setPrimalField (const scalarFieldPtr_Type &primalField)
	Set the primal field vector. More...

void	setDualField (const scalarFieldPtr_Type &dualField)
	Set the dual field vector. More...

void	setFields (const scalarFieldPtr_Type &dualField, const scalarFieldPtr_Type &primalField, const scalarFieldPtr_Type &hybridField)
	Set the fields. More...

void	setDisplayer (const displayerPtr_Type &displayer)
	Set the displayer and, implicitly, the communicator. More...

void	setCommunicator (const commPtr_Type &comm)
	Set the communicator and, implicitly, the displayer. More...

const scalarFieldPtr_Type &	hybridFieldPtr () const
	Returns pointer to the hybrid solution field. More...

scalarFieldPtr_Type &	hybridFieldPtr ()
	Returns pointer to the hybrid solution field. More...

const scalarFieldPtr_Type &	primalFieldPtr () const
	Returns pointer to the primal solution field. More...

scalarFieldPtr_Type &	primalFieldPtr ()
	Returns pointer to the primal solution field. More...

const scalarFieldPtr_Type &	dualFieldPtr () const
	Returns pointer to the dual solution field. More...

scalarFieldPtr_Type &	dualFieldPtr ()
	Returns pointer to the dual solution field. More...

const vectorPtr_Type &	residualPtr () const

vectorPtr_Type &	residualPtr ()

const bcHandlerPtr_Type &	boundaryConditionHandlerPtr () const
	Returns boundary conditions handler. More...

bcHandlerPtr_Type &	boundaryConditionHandlerPtr ()
	Returns boundary conditions handler. More...

const map_Type &	getMap () const
	Returns Epetra local map. More...

const commPtr_Type &	getCommPtr () const
	Returns Epetra communicator. More...

Public Member Functions inherited from DarcySolverTransient< MeshType >
	DarcySolverTransient ()
	Constructor for the class. More...

virtual	~DarcySolverTransient ()
	Virtual destructor. More...

void	setInitialPrimal (const scalarFctPtr_Type &primalInitialFct)
	Initialize primal solution. More...

void	setMass (const scalarFctPtr_Type &massFct)
	Set mass matrix. More...

Protected Member Functions inherited from DarcySolverNonLinear< MeshType >
void	fixedPoint ()
	Perform the fixed point loop to solve the non-linear problem. More...

void	setupNonLinear ()
	Set up the data for the non-linear solver. More...

Protected Member Functions inherited from DarcySolverLinear< MeshType >
	DarcySolverLinear (const darcySolver_Type &)
	Inhibited copy constructor. More...

darcySolver_Type &	operator= (const darcySolver_Type &)
	Inhibited assign operator. More...

virtual void	preLoopElementsComputation ()
	Perform all the operations before doing the loop on volume elements. More...

void	computeConstantMatrices (MatrixElemental &elmatMix)
	Pre-computes local (element independant) matrices. More...

void	staticCondensation (MatrixElemental &localMatrixHybrid, VectorElemental &localVectorHybrid, MatrixElemental &elmatMix, MatrixElemental &elmatReactionTerm, VectorElemental &elvecMix)
	Performs static condensation. More...

void	localComputePrimalAndDual (VectorElemental &localSolution, MatrixElemental &elmatMix, MatrixElemental &elmatReactionTerm, VectorElemental &elvecMix)
	Compute locally, as a post process, the primal and dual variable given the hybrid. More...

void	applyBoundaryConditions ()
	Apply the boundary condition. More...

template<typename MatrixType >
void	symmetrizeMatrix (Int N, MatrixType &A)
	Make matrix symmetric. More...

Protected Member Functions inherited from DarcySolverTransient< MeshType >
virtual void	postComputePrimalAndDual ()
	Do some computation after the calculation of the primal and dual variable. More...

void	setupTime ()
	Setup the time data. More...

Protected Attributes inherited from DarcySolverNonLinear< MeshType >
scalarFieldPtr_Type	M_primalFieldPreviousIteration
	Primal solution at previous iteration step. More...

Protected Attributes inherited from DarcySolverLinear< MeshType >
displayerPtr_Type	M_displayer
	Displayer for parallel cout. More...

dataPtr_Type	M_data
	Data for Darcy solvers. More...

scalarFctPtr_Type	M_scalarSourceFct
	Source function. More...

vectorFctPtr_Type	M_vectorSourceFct
	Vector source function. More...

scalarFctPtr_Type	M_reactionTermFct
	Reaction term function. More...

matrixFctPtr_Type	M_inversePermeabilityFct
	Inverse of the permeability tensor. More...

bcHandlerPtr_Type	M_boundaryConditionHandler
	Bondary conditions handler. More...

scalarFieldPtr_Type	M_primalField
	Primal solution. More...

scalarFieldPtr_Type	M_dualField
	Dual solution. More...

scalarFieldPtr_Type	M_hybridField
	Hybrid solution. More...

matrixPtr_Type	M_matrHybrid
	Hybrid matrix. More...

vectorPtr_Type	M_rhs
	Right hand side. More...

vectorPtr_Type	M_residual
	Residual. More...

solver_Type	M_linearSolver
	Linear solver. More...

preconditionerPtr_Type	M_prec
	Epetra preconditioner for the linear system. More...

Protected Attributes inherited from DarcySolverTransient< MeshType >
timeAdvancePtr_Type	M_timeAdvance
	Time advance. More...

vectorPtr_Type	M_rhsTimeAdvance
	Right hand side coming from the time advance scheme. More...

Detailed Description

template<typename MeshType>
class LifeV::DarcySolverTransientNonLinear< MeshType >

implements a non-linear transient mixed-hybrid FE Darcy solver.

Author: A. Fumagalli aless.nosp@m.io.f.nosp@m.umaga.nosp@m.lli@.nosp@m.mail..nosp@m.poli.nosp@m.mi.it

This class implements a non-linear and transient Darcy solver.

The classical time dependant, non-linear, Darcy formulation is a couple of differential equations of first order with the unknowns 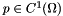$p \in C^1 (\Omega )$ , being the pressure or the primal unknown, and 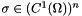$\sigma \in (C^1( \Omega ) )^n$ , being the Darcy velocity or the flux or the dual unknown, such that

$\left\{ \begin{array}{l l l} \Lambda^{-1}(t, p) \sigma + \nabla p = f_v(t) & \mathrm{in} & \Omega \times [0, T]\,, \vspace{0.2cm} \\ \displaystyle \phi \frac{\partial p}{\partial t} + \nabla \cdot \sigma + \pi(t) p - f(t) = 0 & \mathrm{in} & \Omega \times [0, T]\,, \vspace{0.2cm} \\ p = g_D(t) & \mathrm{on} & \Gamma_D \times [0, T]\,,\vspace{0.2cm} \\ \sigma \cdot n + h(t) p = g_R(t) & \mathrm{on} & \Gamma_R \times [0, T]\,. \vspace{0.2cm} \\ p(0) = p_0 & \mathrm{in} & \Omega \end{array} \right.$

The data in the system are:

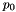the primal variable at initial time;
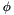$\phi$ the mass term, which does not depend on time;
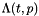$\Lambda(t, p)$ the non linear in 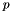permeability tensor;
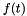the scalar source term;
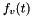the vector source term;
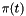$\pi(t)$ the reaction coefficient;
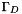$\Gamma_D$ the subset of the boundary of 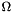$\Omega$ with Dirichlet boundary conditions;
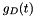Dirichlet boundary condition data;
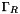$\Gamma_R$ that is the part of the boundary of 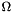$\Omega$ with Robin, or Neumann, boundary conditions;
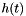and 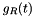Robin boundary condition data;

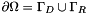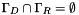We suppose that $\partial \Omega = \Gamma_D \cup \Gamma_R$ and $\Gamma_D \cap \Gamma_R = \emptyset$ .
Using the hybridization procedure, and introducing a new variable, we may split the problem from the entire domain to problems in each elements of the triangulation 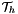$\mathcal{T}_h$ , then we may write the weak formulation for the dual problem. The new variable is the hybrid unknown 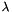$\lambda$ , e.g. "the trace" of pressure of the primal unknown, it is the Lagrange multipliers forcing the continuity of the flux across each faces or edges in the triangulation. We introduce the following functional spaces, the first is the space of the primal variable, the third for the dual variable, the fourth for the hybrid variable.

$\begin{array}{l} V = L^2 (\Omega ) \,,\vspace{0.2cm} \\ H(div, K) = \displaystyle \left\{ \tau \in ( L^2(K))^n : \nabla \cdot \tau \in L^2(K)\right\}\,, \vspace{0.2cm}\\ Z = \displaystyle \left\{ \tau \in L^2(\Omega) : \tau\vert_K \in H(div, K) \, \forall K \in \mathcal{T}_h \right\}\,, \vspace{0.2cm}\\ \Lambda = \displaystyle \left\{ \lambda \in \prod_{K \in \mathcal{T}_h} H^{1/2} (\partial K): \lambda_K = \lambda_{K'} \,\, \mathrm{on} \,\, e_{K-K'} \, \forall K \in \mathcal{T}_h,\, \lambda = g_D \,\, \mathrm{on} \,\, \Gamma_D \right\}\,. \end{array}$

Introducing the following bilinear forms, operator and functionals

$\begin{array}{l l} a(\sigma(t), \tau, p) = \displaystyle \sum_{K \in \mathcal{T}_h}\int_K \Lambda^{-1}(t, p) \sigma \cdot \tau \,, & b(p, \tau) = \displaystyle -\sum_{K \in \mathcal{T}_h} \int_K p \nabla \cdot \tau\,, \vspace{0.2cm}\\ c(\lambda(t), \tau) = \displaystyle \sum_{K \in \mathcal{T}_h} \int_{\partial K} \lambda(t) \tau \cdot n\,,& d(p(t), q) = \displaystyle \sum_{K \in \mathcal{T}_h} \int_{\partial K} \pi(t) p(t) q \,,\vspace{0.2cm}\\ h(\lambda(t), \mu) = \displaystyle \sum_{K \in \mathcal{T}_h} \int_{\partial K \cap \Gamma_R} h \mu \lambda(t) \,,& m(p(t), v) = \displaystyle \sum_{K \in \mathcal{T}_h} \int_K \phi p(t) v \,,\vspace{0.2cm}\\ F(v) = \displaystyle \sum_{K \in \mathcal{T}_h} \int_K f v\,,& F_v(\tau) = \displaystyle \sum_{K \in \mathcal{T}_h} \int_K f_v(t) \tau \,, \vspace{0.2cm}\\ G(\mu) = \displaystyle \sum_{K \in \mathcal{T}_h} \int_{\partial K \cap \Gamma_R} g \mu\,, \end{array}$

we obtain the Darcy problem in the weak form: find 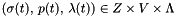$(\sigma(t), \, p(t), \, \lambda(t)) \in Z \times V \times \Lambda$ such that

$\left\{ \begin{array}{l l} a(\sigma(t), \tau, p(t)) + b(p(t), \tau) + c(\lambda(t), \tau) = F_v(\tau) \,, & \forall \tau \in Z \,,\vspace{0.2cm}\\ \displaystyle -\frac{\partial}{\partial t} m(p(t), v) + b(v, \sigma) - d(p(t), v)= -F(v)\,, & \forall v \in V \,,\vspace{0.2cm}\\ c(\mu, \sigma(t)) + h(\lambda(t), \mu) = G(\mu) \,, & \forall \mu \in \Lambda\,. \end{array} \right.$

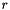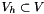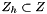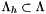
At the semi-discrete level only space discretization is performed, we introduce the polynomial space, of degree $ r $ , that approximate the finite dimensional spaces introduced above $V_h \subset V$ , $Z_h \subset Z$ and $\Lambda_h \subset \Lambda$

$\begin{array}{l} V_h = \displaystyle \left\{ v_h \in V: v_h|_K \in P_r (K)\, \forall K \in \mathcal{T}_h \right\}\,, \vspace{0.2cm}\\ Z_h = \displaystyle \left\{ \tau_h \in Z: \tau_h|_K \in RT_r(K) \, \forall K \in \mathcal{T}_h \right\} \,, \vspace{0.2cm} \\ \Lambda_h = \displaystyle \left\{ \lambda_h \in \Lambda: \lambda_h|_{\partial K} \in R_r( \partial K ) \, \forall K \in \mathcal{T}_h\right\}\,, \end{array}$

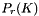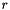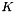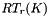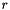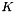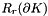where $ P_r(K) $ is the space of polynomial of degree $ r $ in the element $ K $ , $ RT_r(K) $ is the space of polynomial of Raviart-Thomas of degrees $ r $ in the element $ K $ and $R_r(\partial K)$ is the space of polynomial of degree 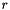$ r $ definite on each of the boundary of the element 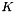$ K $ and discontinuous from one edge to the other.
The finite dimensional problem is: find 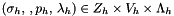$(\sigma_h,\,, p_h, \, \lambda_h) \in Z_h \times V_h \times \Lambda_h$ such that

$\left\{ \begin{array}{l l} a(\sigma_h(t), \tau_h, p_h(t)) + b(p_h(t), \tau_h) + c(\lambda_h(t), \tau_h) = F_v(\tau_h) \,, & \forall \tau_h \in Z_h \,,\vspace{0.2cm}\\ \displaystyle -\frac{\partial}{\partial t} m(p_h(t),v_h) + b(v_h, \sigma_h(t)) - d(p_h(t), v_h) = -F(v_h)\,, & \forall v_h \in V_h \,,\vspace{0.2cm}\\ c(\mu_h, \sigma_h(t)) + h(\lambda_h(t(, \mu_h) = G(\mu_h) \,, & \forall \mu_h \in \Lambda_h\,. \end{array} \right.$

To obatin a fully discrete problem we discretize the time derivative via BDF (backward differentiation formulae) schemes of order 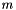$ m $ , with 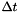$\Delta t$ as time step. Choosing

$p_h^0 = \prod_{V_h} p_0$

we obtain the following system for each 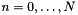$n = 0, \ldots, N$ , with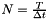 $N = \frac{T}{\Delta t}$

$\left\{ \begin{array}{l l} a(\sigma_h^{n+1}, \tau_h, p_h^{n+1}) + b(p_h^{n+1}, \tau_h) + c(\lambda_h^{n+1}, \tau_h) = F_v(\tau_h)\,, & \forall \tau_h \in Z_h \,,\vspace{0.2cm}\\ \displaystyle -\frac{\alpha_0}{\Delta t} m(p_h^{n+1},v_h) + b(v_h, \sigma_h^{n+1}) - d(p_h^{n+1}, v_h)= -F(v_h) - \frac{1}{\Delta t} m \left( \sum_{i=1}^m \alpha_i p_h^{n+1-i}, v_h \right) \,, & \forall v_h \in V_h \,,\vspace{0.2cm}\\ c(\mu_h, \sigma_h^{n+1}) + h(\lambda_h^{n+1}, \mu_h) = G(\mu_h) \,, & \forall \mu_h \in \Lambda_h\,. \end{array} \right.$

To solve the non-linearity we use a fixed point scheme based on the relative difference between two consecutive iterations of the primal variable. We start from the, user defined, function 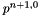$p^{n+1,0}$ and solve the linearized problem for 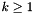$k \geq 1$ : find 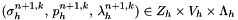$(\sigma_h^{n+1,k},\, p_h^{n+1,k}, \, \lambda_h^{n+1,k}) \in Z_h \times V_h \times \Lambda_h$ such that

$\left\{ \begin{array}{l l} a(\sigma_h^{n+1,k}, \tau_h, p_h^{n+1,k-1}) + b(p_h^{n+1,k}, \tau_h) + c(\lambda_h^{n+1,k}, \tau_h) = F_v(\tau_h)\,, & \forall \tau_h \in Z_h \,,\vspace{0.2cm}\\ \displaystyle -\frac{\alpha_0}{\Delta t} m(p_h^{n+1,k},v_h) + b(v_h, \sigma_h^{n+1,k}) - d(p_h^{n+1,k}, v_h)= -F(v_h) - \frac{1}{\Delta t} m\left( \sum_{i=1}^m \alpha_i p_h^{n+1-i}, v_h \right) \,, & \forall v_h \in V_h \,,\vspace{0.2cm}\\ c(\mu_h, \sigma_h^{n+1,k}) + h(\lambda_h^{n+1,k}, \mu_h) = G(\mu_h) \,, & \forall \mu_h \in \Lambda_h\,. \end{array} \right.$

At each iteration, to solve the linearized problem we use the static condensation procedure, i.e. the unknowns in the discrete weak system are not independent and 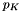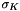$ p_K $ , $\sigma_K$ may be written in function of 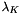$\lambda_K$ alone. We introduce the following local matrices

$\begin{array}{l l l} \left[ A(p_K^{n+1,k-1}) \right]_{ij} = \displaystyle \int_K \Lambda^{-1}(t^{n+1}, p^{n+1,k-1}) \psi_j \cdot \psi_i \,, & \left[ B \right]_{ij} = - \displaystyle \int_K \phi_j \nabla \cdot \psi_i \,, & \left[ C \right]_{ij} = \displaystyle \int_{\partial K} \xi_i \psi_j \cdot n \,, \vspace{0.2cm} \\ \left[ D \right]_{ij} = \displaystyle \int_K \pi(t) \phi_j \phi_i\,, & \left[ H \right]_{ij} = \displaystyle \int_{\partial K \cap \Gamma_R} h \xi_i \xi_j\,, & \left[ M \right]_{ij} = \displaystyle \int_{K} \phi \phi_j \phi_i \,, \vspace{0.2cm} \\ \left[ F \right]_{j} = \displaystyle \int_K f \phi_j\,, & \left[ F_v \right]_{j}= \displaystyle \int_K f_v( (n+1) \Delta t) \cdot \psi_j\,, & \left[ G \right]_{j} = \displaystyle \int_{\partial K \cap \Gamma_R } g \xi_j\,, \end{array}$

where we avoid to write the dependence on the triangle 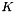$ K $ in all the matrices and vectors.
The local matrix formulation of the finite dimensional problem is

$\left\{ \begin{array}{l} A(p^{n+1,k-1}) \sigma_K^{n+1,k} + B p_K^{n+1,k} + C \lambda_K^{n+1,k} = F_v\,, \vspace{0.2cm} \\ \displaystyle -\frac{\alpha_0}{\Delta t} M p_K^{n+1,k} +B^T \sigma_K^{n+1,k} - D p_K^{n+1,k}= -F - \frac{1}{\Delta t} M \sum_{i=1}^m \alpha_i p_K^{n+1-i} \,, \vspace{0.2cm}\\ C^T \sigma_K^{n+1,k} + H \lambda_K^{n+1,k} = G\,. \end{array} \right.$

Or alternatively

$\begin{array}{l l l} \left[ \begin{array}{c c c} A(p_K^{n+1,k-1}) & B & C \vspace{0.2cm} \\ B^T & \displaystyle -\frac{\alpha_0}{\Delta t} M -D& 0 \vspace{0.2cm} \\ C^T & 0 & H \end{array} \right] \, \cdot & \left[ \begin{array}{c} \sigma_K^{n+1,k} \vspace{0.2cm}\\ p_K^{n+1,k} \vspace{0.2cm}\\ \lambda_K^{n+1,K} \end{array} \right] \, & = \left[ \begin{array}{c} F_v \vspace{0.2cm}\\ \displaystyle -F - \frac{1}{\Delta t} M \sum_{i=1}^m \alpha_i p_K^{n+1-i} \vspace{0.2cm}\\ G \end{array} \right]\,. \end{array}$

Introducing the local hybrid matrix and local hybrid right hand side

$\begin{array}{l} \displaystyle L_K = -C^T A^{-1}( p_k^{n+1,k-1}) C + C^T A^{-1}( p_k^{n+1,k-1}) B \left( \frac{\alpha_0}{\Delta t} M + B^T A^{-1}( p_k^{n+1,k-1}) B + D \right)^{-1} B^T A^{-1}( p_k^{n+1,k-1}) C + H \,, \vspace{0.2cm} \\ \displaystyle r_K = G + C^T A^{-1}( p_k^{n+1,k-1}) B \left( \frac{\alpha_0}{\Delta t} + B^T A^{-1}( p_k^{n+1,k-1}) B + D\right)^{-1} F + C^T A^{-1}( p_k^{n+1,k-1}) B \left( \frac{\alpha_0}{\Delta t}M + B^T A^{-1}( p_k^{n+1,k-1}) B + D \right)^{-1} B^T A^{-1}( p_k^{n+1,k-1}) F_v - C^T A^{-1}( p_k^{n+1,k-1}) F_v \,, \end{array}$

Imposing that at each edge or face the hybrid unknown is single value we obtain a linear system for the hybrid unknown

$L \lambda^{n+1,k} = r \,.$

We recover the primal and dual variable as a post-process from the hybrid variable at element level, so we have

$\begin{array}{l} \displaystyle p_K^{n+1,k} = \left( \frac{\alpha_0}{\Delta t} M + B^T A^{-1}( p_k^{n+1,k-1}) B + D \right)^{-1} \left( F + \frac{1}{\Delta t} M \sum_{i=1}^m \alpha_i p_K^{n+1-i} - B^T A^{-1}( p_k^{n+1,k-1}) C \lambda_K^{n+1,k} \right)\,, \vspace{0.2cm} \\ \displaystyle \sigma_K^{n+1,k} = -A^{-1} ( p_k^{n+1,k-1})( B p_K^{n+1,k} + C \lambda_K^{n+1,k} ) \,. \end{array}$

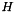Note: In the code we do not use the matrix and the vector 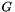, because all the boundary conditions are imposed via BCHandler class.; Example of usage can be found in darcy_nonlinear and darcy_linear. Coupled with an hyperbolic solver in impes.

Todo:: Insert any scientific publications that use this solver.

Definition at line 260 of file DarcySolverTransientNonLinear.hpp.

Member Typedef Documentation

◆ mesh_Type

typedef MeshType mesh_Type

Typedef for mesh template.

Definition at line 272 of file DarcySolverTransientNonLinear.hpp.

◆ darcySolverTransientNonLinear_Type

typedef DarcySolverTransientNonLinear< mesh_Type > darcySolverTransientNonLinear_Type

Self typedef.

Definition at line 275 of file DarcySolverTransientNonLinear.hpp.

◆ darcySolverLinear_Type

typedef DarcySolverLinear< mesh_Type > darcySolverLinear_Type

Darcy solver class.

Definition at line 278 of file DarcySolverTransientNonLinear.hpp.

◆ darcySolverNonLinear_Type

typedef DarcySolverNonLinear< mesh_Type > darcySolverNonLinear_Type

Darcy non linear solver class.

Definition at line 281 of file DarcySolverTransientNonLinear.hpp.

◆ darcySolverTransient_Type

typedef DarcySolverTransient< mesh_Type > darcySolverTransient_Type

Darcy transient solver class.

Definition at line 284 of file DarcySolverTransientNonLinear.hpp.

◆ data_Type

typedef darcySolverLinear_Type::data_Type data_Type

Typedef for the data type.

Definition at line 287 of file DarcySolverTransientNonLinear.hpp.

◆ dataPtr_Type

typedef darcySolverLinear_Type::dataPtr_Type dataPtr_Type

Shared pointer for the data type.

Definition at line 290 of file DarcySolverTransientNonLinear.hpp.

◆ matrixFctPtr_Type

typedef darcySolverLinear_Type::matrixFctPtr_Type matrixFctPtr_Type

Shared pointer to a matrix value function.

Definition at line 293 of file DarcySolverTransientNonLinear.hpp.

◆ vector_Type

typedef darcySolverLinear_Type::vector_Type vector_Type

Distributed vector.

Definition at line 296 of file DarcySolverTransientNonLinear.hpp.

Constructor & Destructor Documentation

◆ DarcySolverTransientNonLinear() [1/2]

DarcySolverTransientNonLinear ( )

Constructor for the class.

Definition at line 413 of file DarcySolverTransientNonLinear.hpp.

Here is the caller graph for this function:

◆ ~DarcySolverTransientNonLinear()

virtual ~DarcySolverTransientNonLinear ( )

inlinevirtual

Virtual destructor.

Definition at line 307 of file DarcySolverTransientNonLinear.hpp.

◆ DarcySolverTransientNonLinear() [2/2]

DarcySolverTransientNonLinear ( const darcySolverTransientNonLinear_Type & )

protected

Inhibited copy constructor.

Member Function Documentation

◆ setup()

void setup ( )

virtual

Set up the linear solver, the preconditioner for the linear system and the exporter to save the solution.

Reimplemented from DarcySolverNonLinear< MeshType >.

Definition at line 430 of file DarcySolverTransientNonLinear.hpp.

◆ solve()

void solve ( )

virtual

Solve the problem calling the non linear solver.

Reimplemented from DarcySolverNonLinear< MeshType >.

Definition at line 446 of file DarcySolverTransientNonLinear.hpp.

◆ setInversePermeability()

void setInversePermeability ( const matrixFctPtr_Type & invPerm )

inlinevirtual

Set the inverse of diffusion tensor.

Parameters

invPerm Inverse of the permeability tensor for the problem.

Reimplemented from DarcySolverNonLinear< MeshType >.

Definition at line 330 of file DarcySolverTransientNonLinear.hpp.

◆ operator=()

darcySolverTransientNonLinear_Type& operator= ( const darcySolverTransientNonLinear_Type & )

protected

Inhibited assign operator.

◆ resetVariables()

virtual void resetVariables ( )

inlineprotectedvirtual

Update all problem variables.

Update all the variables of the problem before the construction of the global hybrid matrix, e.g. reset the global hybrid matrix. It is principally used for a time dependent derived class.

Reimplemented from DarcySolverNonLinear< MeshType >.

Definition at line 365 of file DarcySolverTransientNonLinear.hpp.

◆ localMatrixComputation()

virtual void localMatrixComputation	(	const UInt &	iElem,
		MatrixElemental &	elmatMix,
		MatrixElemental &	elmatReactionTerm
	)

inlineprotectedvirtual

Compute elementary matrices.

Locally update the current finite element for the dual finite element space, then compute the Hdiv mass matrix.

Parameters

iElem	Id of the current geometrical element.
elmatMix	The local matrix in mixed form.
elmatReactionTerm	The local matrix for the reaction term.

Reimplemented from DarcySolverTransient< MeshType >.

Definition at line 378 of file DarcySolverTransientNonLinear.hpp.

◆ localVectorComputation()

virtual void localVectorComputation	(	const UInt &	iElem,
		VectorElemental &	elvecMix
	)

inlineprotectedvirtual

Computes local vectors.

Call the Darc_y solver localVectorComputation method and compute the additional scalar vector for the time dependent term.

Parameters

iElem	Id of the current geometrical element.
elvecMix	The local vector in mixed form.

Reimplemented from DarcySolverTransient< MeshType >.

Definition at line 392 of file DarcySolverTransientNonLinear.hpp.

The documentation for this class was generated from the following file:

DarcySolverTransientNonLinear.hpp

Public Types

Constructors & destructor

Methods

Set methods

Private Constructors

Private Operators

Protected Methods

Additional Inherited Members

Detailed Description

template<typename MeshType> class LifeV::DarcySolverTransientNonLinear< MeshType >

Member Typedef Documentation

◆ mesh_Type

◆ darcySolverTransientNonLinear_Type

◆ darcySolverLinear_Type

◆ darcySolverNonLinear_Type

◆ darcySolverTransient_Type

◆ data_Type

◆ dataPtr_Type

◆ matrixFctPtr_Type

◆ vector_Type

Constructor & Destructor Documentation

◆ DarcySolverTransientNonLinear() [1/2]

◆ ~DarcySolverTransientNonLinear()

◆ DarcySolverTransientNonLinear() [2/2]

Member Function Documentation

◆ setup()

◆ solve()

◆ setInversePermeability()

◆ operator=()

◆ resetVariables()

◆ localMatrixComputation()

◆ localVectorComputation()

template<typename MeshType>
class LifeV::DarcySolverTransientNonLinear< MeshType >