 |
LifeV
|
 |
LifeV
|
class TimeAdvanceBDF - Backward differencing formula time discretization for the first and the second order problem in time. More...
#include <TimeAdvanceBDF.hpp>
 Inheritance diagram for TimeAdvanceBDF< feVectorType >:
Inheritance diagram for TimeAdvanceBDF< feVectorType >: Collaboration diagram for TimeAdvanceBDF< feVectorType >:
Collaboration diagram for TimeAdvanceBDF< feVectorType >:Public Types | |
| typedef TimeAdvance< feVectorType > | super |
| class super More... | |
| typedef super::feVector_Type | feVector_Type |
| type of template More... | |
| typedef super::feVectorContainer_Type | feVectorContainer_Type |
| container of feVector More... | |
| typedef super::feVectorContainerPtr_Type | feVectorContainerPtr_Type |
| container of pointer of feVector; More... | |
| typedef feVectorContainerPtr_Type::iterator | feVectorContainerPtrIterate_Type |
| iterator; More... | |
| typedef super::feVectorSharedPtrContainer_Type | feVectorSharedPtrContainer_Type |
| container of pointer of feVector; More... | |
Constructor & Destructor | |
| TimeAdvanceBDF () | |
| Empty Constructor. More... | |
| virtual | ~TimeAdvanceBDF () |
| Destructor. More... | |
Methods | |
| void | shiftRight (const feVector_Type &solution) |
| Update the state vector. More... | |
| void | RHSFirstDerivative (const Real &timeStep, feVectorType &rhsContribution) const |
Update the right hand side 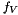 of the time derivative formula. More... of the time derivative formula. More... | |
| void | updateRHSSecondDerivative (const Real &timeStep=1) |
Update the right hand side 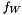 of the time derivative formula. More... of the time derivative formula. More... | |
| void | showMe (std::ostream &output=std::cout) const |
| Show the properties of temporal scheme. More... | |
Set Methods | |
| void | setup (const UInt &order, const UInt &orderDerivative=1) |
| Initialize the parameters of time advance scheme. More... | |
| void | setup (const std::vector< Real > &, const UInt &) |
| Initialize the parameters of time advance scheme used in TimeAdvanceNewmark. More... | |
| void | setInitialCondition (const feVector_Type &x0) |
| Initialize the StateVector. More... | |
| void | setInitialCondition (const feVector_Type &, const feVector_Type &) |
| Initialize the StateVector used in TimeAdvanceNewmark. More... | |
| void | setInitialCondition (const feVector_Type &, const feVector_Type &, const feVector_Type &) |
| Initialize the StateVector used in TimeAdvanceNewmark. More... | |
| void | setInitialCondition (const feVectorSharedPtrContainer_Type &x0) |
| Initialize all the entries of the unknown vector to be derived with a. More... | |
Get Methods | |
| Real | coefficientExtrapolation (const UInt &i) const |
Return the 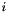 -th coefficient of the unk's extrapolation. More... -th coefficient of the unk's extrapolation. More... | |
| Real | coefficientExtrapolationFirstDerivative (const UInt &i) const |
Return the 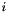 -th coefficient of the velocity's extrapolation. More... -th coefficient of the velocity's extrapolation. More... | |
| void | extrapolation (feVector_Type &extrapolation) const |
| Compute the polynomial extrapolation of solution. More... | |
| void | extrapolationFirstDerivative (feVector_Type &extrapolation) const |
| Compute the polynomial extrapolation of velocity. More... | |
| feVectorType | firstDerivative () const |
| Return the current velocity. More... | |
| feVectorType | secondDerivative () const |
| Return the current acceleration. More... | |
Additional Inherited Members | |
 Public Types inherited from TimeAdvance< feVectorType > Public Types inherited from TimeAdvance< feVectorType > | |
| typedef feVectorType | feVector_Type |
| typedef ScalarVector | container_Type |
| typedef std::vector< feVector_Type > | feVectorContainer_Type |
| typedef std::vector< feVector_Type * > | feVectorContainerPtr_Type |
| typedef feVectorContainerPtr_Type::iterator | feVectorContainerPtrIterate_Type |
| typedef std::vector< std::shared_ptr< feVector_Type > > | feVectorSharedPtrContainer_Type |
 Public Member Functions inherited from TimeAdvance< feVectorType > Public Member Functions inherited from TimeAdvance< feVectorType > | |
| TimeAdvance () | |
| Empty Constructor. More... | |
| virtual | ~TimeAdvance () |
| Destructor. More... | |
class TimeAdvanceBDF - Backward differencing formula time discretization for the first and the second order problem in time.
First order problem
A differential equation of the form
![\[ M \dot{u} + A u = f \]](form_148.png)
is discretizated in time as
![\[ M V_{k+1} + A U_{k+1} = f_{k+1} \]](form_149.png)
where V denotes the polynomial of order n in t that interpolates 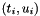 for
for 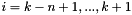 .
.
The approximative time derivative 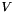 is a linear combination of state vectors
is a linear combination of state vectors 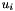 :
:
![\[ V_{k+1} = \frac{1}{\Delta t} (\alpha_0 U_{k+1} - \sum_{i=0}^n \alpha_i U_{k+1-i} )\]](form_154.png)
Thus we have
![\[ \frac{\alpha_0}{\Delta t} M U_{k+1} = A U_{k+1} + f + M f_V \]](form_155.png)
with
![\[ f_V= \frac{1}{\Delta t} \sum_{i=1}^n \alpha_i U_{k+1-i} \]](form_156.png)
This class stores the n last state vectors in order to be able to calculate 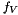 . It also provides
. It also provides 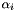 and can extrapolate the the new state from the
and can extrapolate the the new state from the 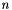 last states with a polynomial of order
last states with a polynomial of order  :
:
![\[ U_{k+1} \approx \sum_{i=0}^{n-1} \beta_i U_{k-i} \]](form_160.png)
Second order problem
A differential equation of the form
![\[ M \ddot{u}= D( u, \dot{u}) + A(u) + f \]](form_161.png)
is discretized in time as
![\[ M W_{k+1} = A(U^*) U_{k+1} +D(U^*, V^*) V_{k+1} + f_{k+1} \]](form_162.png)
where 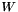 and
and 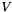 denotes the polynomial of order
denotes the polynomial of order 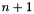 and order
and order 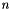 , while
, while 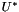 and
and 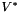 are suitable extrapolations.
are suitable extrapolations.
The velocity vector, as for first order problem, is:
![\[ V_{k+1} = \frac{1}{\Delta t} (\alpha_0 U_{k+1} - \sum_{i=0}^n \alpha_i U_{k+1-i} )\]](form_154.png)
while the acceleration vector 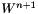 is:
is:
![\[ W_{k+1} = \frac{1}{\Delta t^2} (\xi_0 U_{k+1} - \sum_{i=0}^{n+1} \xi_i U_{k+1-i} )\]](form_165.png)
Thus we have
![\[ \frac{\xi_0}{\Delta t^2} M U_{k+1} + \frac{\alpha_0}{\Delta t } D U_{k+1} + A U_{k+1} + f + M f_W + D f_V \]](form_166.png)
with
![\[ f_V= \frac{1}{\Delta t} \sum_{i=1}^n \alpha_i U_{k+1-i} \]](form_156.png)
and
![\[ f_W =\frac{1}{\Delta t^2} \sum_{i=1}^{n+1} \xi_i U_{ k+1 - i} \]](form_167.png)
It also provides 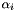 and can extrapolate the the new state from the
and can extrapolate the the new state from the 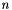 last states with a polynomial of order
last states with a polynomial of order  :
:
![\[ U_{k+1} \approx U^*= \sum_{i=0}^{n-1} \beta_i U_{k-i} \]](form_168.png)
and 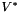 in following way:
in following way:
![\[ V_{k+1} \approx V^*=\sum_{i=0}^p \frac{\beta_i^V}{\Delta t} U^{n-i} = W^{n+1}+O(\Delta t^p), \]](form_169.png)
Definition at line 140 of file TimeAdvanceBDF.hpp.
| typedef TimeAdvance< feVectorType > super |
class super
Definition at line 149 of file TimeAdvanceBDF.hpp.
| typedef super::feVector_Type feVector_Type |
type of template
Definition at line 151 of file TimeAdvanceBDF.hpp.
container of feVector
Definition at line 154 of file TimeAdvanceBDF.hpp.
container of pointer of feVector;
Definition at line 157 of file TimeAdvanceBDF.hpp.
| typedef feVectorContainerPtr_Type::iterator feVectorContainerPtrIterate_Type |
iterator;
Definition at line 160 of file TimeAdvanceBDF.hpp.
container of pointer of feVector;
Definition at line 163 of file TimeAdvanceBDF.hpp.
| TimeAdvanceBDF | ( | ) |
Empty Constructor.
Definition at line 304 of file TimeAdvanceBDF.hpp.
|
inlinevirtual |
Destructor.
Definition at line 175 of file TimeAdvanceBDF.hpp.
|
virtual |
Update the state vector.
Update the vectors of the previous time steps by shifting on the right the old values.
| solution | current (new) value of the state vector |
Implements TimeAdvance< feVectorType >.
Definition at line 314 of file TimeAdvanceBDF.hpp.
| void RHSFirstDerivative | ( | const Real & | timeStep, |
| feVectorType & | rhsContribution | ||
| ) | const |
Update the right hand side 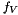 of the time derivative formula.
of the time derivative formula.
Return the right hand side 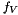 of the time derivative formula
of the time derivative formula
| timeStep | defined the time step need to compute the |
Definition at line 337 of file TimeAdvanceBDF.hpp.
| void updateRHSSecondDerivative | ( | const Real & | timeStep = 1 | ) |
Update the right hand side 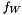 of the time derivative formula.
of the time derivative formula.
Sets and Returns the right hand side 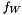 of the time derivative formula
of the time derivative formula
| timeStep | defined the time step need to compute the 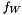 |
Definition at line 351 of file TimeAdvanceBDF.hpp.
| void showMe | ( | std::ostream & | output = std::cout | ) | const |
Show the properties of temporal scheme.
Definition at line 370 of file TimeAdvanceBDF.hpp.
Initialize the parameters of time advance scheme.
Initialize parameters of time advance scheme;
| order | define the order of BDF; |
| orderDerivative | define the order of derivate; |
Definition at line 403 of file TimeAdvanceBDF.hpp.
Initialize the parameters of time advance scheme used in TimeAdvanceNewmark.
Definition at line 224 of file TimeAdvanceBDF.hpp.
| void setInitialCondition | ( | const feVector_Type & | x0 | ) |
Initialize the StateVector.
Initialize all the entries of the unknown vector to be derived with the vector x0 (duplicated). this class is virtual because used in BDF;
| x0 | is the initial unk; |
Definition at line 526 of file TimeAdvanceBDF.hpp.
|
inline |
Initialize the StateVector used in TimeAdvanceNewmark.
Definition at line 238 of file TimeAdvanceBDF.hpp.
|
inline |
Initialize the StateVector used in TimeAdvanceNewmark.
Definition at line 244 of file TimeAdvanceBDF.hpp.
| void setInitialCondition | ( | const feVectorSharedPtrContainer_Type & | x0 | ) |
Initialize all the entries of the unknown vector to be derived with a.
set of vectors x0
initialize zero
Definition at line 551 of file TimeAdvanceBDF.hpp.
Return the 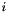 -th coefficient of the unk's extrapolation.
-th coefficient of the unk's extrapolation.
Definition at line 606 of file TimeAdvanceBDF.hpp.
Return the 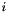 -th coefficient of the velocity's extrapolation.
-th coefficient of the velocity's extrapolation.
Definition at line 616 of file TimeAdvanceBDF.hpp.
| void extrapolation | ( | feVector_Type & | extrapolation | ) | const |
Compute the polynomial extrapolation of solution.
Compute the polynomial extrapolation approximation of order  of
of 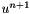 defined by the n stored state vectors
defined by the n stored state vectors
Definition at line 626 of file TimeAdvanceBDF.hpp.
| void extrapolationFirstDerivative | ( | feVector_Type & | extrapolation | ) | const |
Compute the polynomial extrapolation of velocity.
Compute the polynomial extrapolation approximation of order  of
of 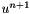 defined by the n stored state vectors
defined by the n stored state vectors
Definition at line 638 of file TimeAdvanceBDF.hpp.
| feVectorType firstDerivative | ( | ) | const |
Return the current velocity.
Definition at line 653 of file TimeAdvanceBDF.hpp.
| feVectorType secondDerivative | ( | ) | const |
Return the current acceleration.
Definition at line 681 of file TimeAdvanceBDF.hpp.