#include <darcy.hpp>

Collaboration diagram for darcy_linear:

Data Structures
struct	Private
	Private Members. More...

Private Attributes
std::shared_ptr< Private >	Members

	darcy_linear (int argc, char **argv)
	Constructor. More...

	~darcy_linear ()
	Destructor. More...

LifeV::Real	run ()
	To lunch the simulation. More...

Detailed Description

Includes.

LifeV linear Darcy test case

Author: A. Fumagalli aless.nosp@m.io.f.nosp@m.umaga.nosp@m.lli@.nosp@m.mail..nosp@m.poli.nosp@m.mi.it

Simple linear 3D Darcy test with Dirichlet, Neumann and Robin Boundary condition.
Solve the problem in dual-mixed form

$\left\{ \begin{array}{l l l } \Lambda^{-1} \sigma + \nabla p = f_v & \mathrm{in} & \Omega, \vspace{0.2cm} \\ \nabla \cdot \sigma + \pi p - f = 0 & \mathrm{in} & \Omega, \vspace{0.2cm} \\ p = g_D & \mathrm{on} & \Gamma_D,\vspace{0.2cm} \\ \sigma \cdot n + h p = g_R & \mathrm{on} & \Gamma_R, \vspace{0.2cm} \\ \sigma \cdot n = g_N & \mathrm{on} & \Gamma_N, \end{array} \right.$

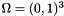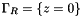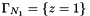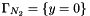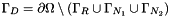where $\Omega = (0,1)^3$ with $\Gamma_R = \left\{ z = 0 \right\}$ , $\Gamma_{N_1} = \left\{ z = 1 \right\}$ , $\Gamma_{N_2} = \left\{ y = 0 \right\}$ and $\Gamma_D = \partial \Omega \setminus \left( \Gamma_R \cup \Gamma_{N_1} \cup \Gamma_{N_2} \right)$ . Furthermore the data are

$\begin{array}{l l l} f_v(x,y,z) = \left( x^3, 2y, 4z \right)^T & \pi(x,y,z) = xy - 0.5z & f(x,y,z) = 4x^2 - 4y^2 - 8xy + 6 + (xy - 0.5z)(x^2y^2 + 6x + 5z), \vspace{0.2cm} \\ g_D(x,y,z) = x^2y^2 + 6x + 5z, & h(x,y,z) = 1, & g_R(x,y,z) = 5 - 4z + x^2y^2 + 6x + 5z, \vspace{0.2cm} \\ g_{N_1}(x,y,z) = - 5 + 4z, & g_{N_2}(x,y,z) = 2xy^2 + 6 + 2x^2y - 2y - x^3, & \Lambda (x,y,z) = \left( \begin{array}{c c c} 2 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right). \end{array}$

The analytical solutions are

$p(x,y,z) = x^2y^2 + 6x + 5z, \quad \sigma(x,y,z) = \left( \begin{array}{c} - 4xy^2 - 12 - 2x^2y + 2x^3 + 2y \\ -2xy^2 - 6 - 2x^2y + 2y + x^3 \\ - 5 + 4z \end{array} \right).$

The computed errors are

N	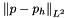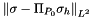$\left\Vert p - p_h \right\Vert_{L^2}$	$\left\Vert \sigma - \Pi_{P_0} \sigma_h \right\Vert_{L^2}$	N proc
5	0.338269	0.411764	3
10	0.166443	0.204983	3
20	0.0832153	0.102579	3
40	0.0416069	0.051361	32
80	0.0208047	0.0258553	96

where N is the number of subdivisions for each boundary.

Example of the solution with N = 5.

Definition at line 152 of file 3d/darcy.hpp.

Constructor & Destructor Documentation

◆ darcy_linear()

darcy_linear	(	int	argc,
		char **	argv
	)

Constructor.

Constructors.

Definition at line 106 of file 3d/darcy.cpp.

Here is the caller graph for this function:

◆ ~darcy_linear()

~darcy_linear ( )

inline

Destructor.

Definition at line 167 of file 3d/darcy.hpp.

Member Function Documentation

◆ run()

Real run ( )

To lunch the simulation.

Methods.

Definition at line 130 of file 3d/darcy.cpp.

Field Documentation

◆ Members

std::shared_ptr<Private> Members

private

Definition at line 182 of file 3d/darcy.hpp.

The documentation for this class was generated from the following files:

Data Structures

Private Attributes