 |
LifeV
|
 |
LifeV
|
Includes. More...
#include <darcy.hpp>
 Collaboration diagram for darcy_nonlinear:
Collaboration diagram for darcy_nonlinear:Data Structures | |
| struct | Private |
| Private Members. More... | |
Private Attributes | |
| std::shared_ptr< Private > | Members |
| darcy_nonlinear (int argc, char **argv) | |
| Constructor. More... | |
| ~darcy_nonlinear () | |
| Destructor. More... | |
| LifeV::Real | run () |
| To lunch the simulation. More... | |
Includes.
LifeV non-linear and transient Darcy test case
A 2D Darcy transient and non-linear test with Dirichlet boundary condition. Let us set 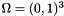 and
and 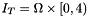 , solve the problem in dual-mixed form
, solve the problem in dual-mixed form
![\[ \left\{ \begin{array}{l l l } \Lambda^{-1} \left( p \right) \sigma + \nabla p = f_v & \mathrm{in} & I_T, \vspace{0.2cm} \\ \displaystyle \phi \frac{\partial p}{\partial t} + \nabla \cdot \sigma + \pi p - f = 0 & \mathrm{in} & I_T, \vspace{0.2cm} \\ p = g_D & \mathrm{on} & \partial \Omega \times [0,4),\vspace{0.2cm} \\ p = p_0 & \mathrm{in} & \Omega. \end{array} \right. \]](form_369.png)
Furthermore the data are
![\[ \begin{array}{l l l} f_v(x,y) = \left( ty - tx, -t^2 y^2 \right)^T & \pi(x,y) = 1 & f(x,y) = tx^2 - 2t^2 - t - (6y + 2 t^2 y)(1 + t^4 x^4 + y^6 + 2 t^2 x^2 y^3) - (3y^2 + t^2 y^2)(6y^5 + 6t^2 x^2 y^2) + t^2 x^2 + y^3, \vspace{0.2cm} \\ g_D(x,y,z) = t^2 x^2 + y^3, & \phi(x,y) = 0.5, & \Lambda (x,y,p) = \left( \begin{array}{c c} 1 & 0 \\ 0 & 1+p^2 \end{array} \right), \\ p_0(x,y) = y^3. & & \end{array} \]](form_370.png)
The analytical solutions are
![\[ p(x,y,z) = t^2 x^2 + y^3, \quad \sigma(x,y,z) = \left( \begin{array}{c} - 2t^2 x + t (y - x) \\ - (3y^2 + t^2 y^2)( 1 + t^4 x^4 + y^6 +2 t^2 x^2 y^3) \end{array} \right). \]](form_371.png)
Fixing 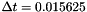 and the tolerance of the fixed point scheme at
and the tolerance of the fixed point scheme at 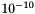 , the computed space errors are
, the computed space errors are
| N | 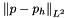 | 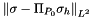 | N proc |
|---|---|---|---|
| 10 | 0.105324 | 0.284968 | 8 |
| 20 | 0.0375415 | 0.140317 | 8 |
| 40 | 0.0162273 | 0.066338 | 16 |
| 80 | 0.00773563 | 0.0315562 | 16 |
| 160 | 0.00381641 | 0.015142 | 32 |
where N is the number of subdivisions for each boundary.
Definition at line 143 of file 2d/darcy.hpp.
| darcy_nonlinear | ( | int | argc, |
| char ** | argv | ||
| ) |
Constructor.
Constructors.
Definition at line 110 of file 2d/darcy.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Destructor.
Definition at line 158 of file 2d/darcy.hpp.
| Real run | ( | ) |
|
private |
Definition at line 173 of file 2d/darcy.hpp.