 |
LifeV
|
 |
LifeV
|
TimeAdvanceNewmark - Class to deal the 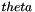 -method and TimeAdvanceNewmark scheme.
More...
-method and TimeAdvanceNewmark scheme.
More...
#include <TimeAdvanceNewmark.hpp>
 Inheritance diagram for TimeAdvanceNewmark< feVectorType >:
Inheritance diagram for TimeAdvanceNewmark< feVectorType >: Collaboration diagram for TimeAdvanceNewmark< feVectorType >:
Collaboration diagram for TimeAdvanceNewmark< feVectorType >:Private Attributes | |
| Real | M_theta |
Coefficient of TimeAdvanceNewmark: 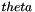 . More... . More... | |
| Real | M_gamma |
Coefficient of TimeAdvanceNewmark: 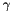 . More... . More... | |
Public Types | |
| typedef TimeAdvance< feVectorType > | super |
| typedef super::feVector_Type | feVector_Type |
| typedef super::feVectorContainer_Type | feVectorContainer_Type |
| typedef super::feVectorContainerPtr_Type | feVectorContainerPtr_Type |
| typedef feVectorContainerPtr_Type::iterator | feVectorContainerPtrIterate_Type |
| typedef super::feVectorSharedPtrContainer_Type | feVectorSharedPtrContainer_Type |
Constructor & Destructor | |
| TimeAdvanceNewmark () | |
| Empty Constructor. More... | |
| virtual | ~TimeAdvanceNewmark () |
| Destructor. More... | |
Methods | |
| void | shiftRight (const feVector_Type &solution) |
| Update the state vector. More... | |
| void | RHSFirstDerivative (const Real &timeStep, feVectorType &rhsContribution) const |
Update the right hand side 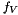 of the time derivative formula. More... of the time derivative formula. More... | |
| void | updateRHSSecondDerivative (const Real &timeStep=1) |
Update the right hand side 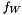 of the time derivative formula. More... of the time derivative formula. More... | |
| void | showMe (std::ostream &output=std::cout) const |
| Show the properties of temporal scheme. More... | |
Set Methods | |
| void | setup (const UInt &, const UInt &) |
| Initialize the parameters of time advance scheme. More... | |
| void | setup (const std::vector< Real > &coefficients, const UInt &orderDerivative) |
| Initialize the parameters of time advance scheme. More... | |
| void | setInitialCondition (const feVector_Type &x0) |
| Initialize the StateVector. More... | |
| void | setInitialCondition (const feVector_Type &x0, const feVector_Type &v0) |
| initialize the state vector More... | |
| void | setInitialCondition (const feVector_Type &x0, const feVector_Type &v0, const feVector_Type &w0) |
| initialize the state vector More... | |
| void | setInitialCondition (const feVectorSharedPtrContainer_Type &x0) |
| Initialize the state vector. More... | |
Get Methods | |
| Real | coefficientExtrapolation (const UInt &i) const |
Return the 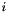 -th coefficient of the unk's extrapolation. More... -th coefficient of the unk's extrapolation. More... | |
| Real | coefficientExtrapolationFirstDerivative (const UInt &i) const |
Return the 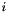 -th coefficient of the velocity's extrapolation. More... -th coefficient of the velocity's extrapolation. More... | |
| void | extrapolation (feVector_Type &extrapolation) const |
| Compute the polynomial extrapolation of solution. More... | |
| void | extrapolationFirstDerivative (feVector_Type &extrapolation) const |
| Compute the polynomial extrapolation of velocity. More... | |
| feVector_Type | firstDerivative () const |
| Return the current velocity. More... | |
| feVector_Type | secondDerivative () const |
| Return the current acceleration. More... | |
Additional Inherited Members | |
 Public Types inherited from TimeAdvance< feVectorType > Public Types inherited from TimeAdvance< feVectorType > | |
| typedef feVectorType | feVector_Type |
| typedef ScalarVector | container_Type |
| typedef std::vector< feVector_Type > | feVectorContainer_Type |
| typedef std::vector< feVector_Type * > | feVectorContainerPtr_Type |
| typedef feVectorContainerPtr_Type::iterator | feVectorContainerPtrIterate_Type |
| typedef std::vector< std::shared_ptr< feVector_Type > > | feVectorSharedPtrContainer_Type |
 Public Member Functions inherited from TimeAdvance< feVectorType > Public Member Functions inherited from TimeAdvance< feVectorType > | |
| TimeAdvance () | |
| Empty Constructor. More... | |
| virtual | ~TimeAdvance () |
| Destructor. More... | |
TimeAdvanceNewmark - Class to deal the 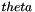 -method and TimeAdvanceNewmark scheme.
-method and TimeAdvanceNewmark scheme.
This class can be used to approximate problems of the first order and the second order in time. In the first case the temporal scheme is a theta-method, while in the second case is a TimeAdvanceNewmark scheme.
This class defines the state vector 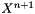 , a suitable extrapolation of vector
, a suitable extrapolation of vector 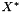 and opportune coefficients used to determinate
and opportune coefficients used to determinate 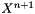 and
and 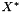 .
.
First order problem:
![\[ M u' + A(u) = f \]](form_191.png)
the state vector is
![\[X^{n+1} = (U^{n+1},V^{n+1}, U^{n}, V^{n})\]](form_192.png)
. where 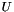 is an approximation of
is an approximation of 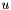 and
and 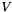 of
of 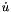 .
.
We consider a parameter 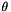 , and we apply the following theta method:
, and we apply the following theta method:
![\[ U^{n+1} = U^{n} + \Delta t \theta V^{n+1} + (1 − \theta) V^n, \]](form_194.png)
so the approximation of velocity at timestep 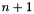 is:
is:
![\[ V^{ n+1} = 1/ (\theta * \Delta t) (U^{n+1}-U^n)+( 1 - 1 / \theta) V^n;\]](form_195.png)
We can linearize non-linear term 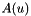 as
as 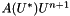 , where the
, where the 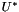 becomes:
becomes:
![\[ U^∗ = U^n + \Delta t V^n, \]](form_198.png)
The coefficients 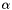 ,
, 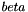 depend on
depend on 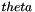 , and we can use a explicit
, and we can use a explicit 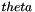 -method.
-method.
Second order Method:
![\[ M \ddot{u} + D(u, \dot{u})+ A(u) = f \]](form_201.png)
the state vector is \form#202 where U is an approximation of \form#193 and \form#121 of \form#122 and \form#137 of \form#203 . We introduce the parameters ( \form#189, \form#188) and we apply the following TimeAdvanceNewmark method:
![\[ U^{n+1} = U^{n} + \Delta t \theta V^{n+1} + (1 − \theta) V^n, \]](form_194.png)
so the approximation of velocity at time step \form#123 is
![\[ V^{ n+1} = \beta / (\theta * \Delta t) (U^{n+1}-U^n)+( 1 - \gamma/ \theta) V^n+ (1- \gamma /(2\theta)) \Delta t W^n;\]](form_204.png)
and we determine \form#164 by
![\[ W^{n+1} =1/(\theta \Delta t^2) (U^{n+1}-U^{n}) - 1 / \Delta t V^n + (1-1/(2\theta)) W^n \]](form_205.png)
.
We can linearize non-linear term \form#196 as \form#197 and \form#206 as \form#207, where \form#144 is given by
![\[ U^∗ = U^n + \Delta t V^n \]](form_208.png)
and \form#145 is
![\[ V^* =V^n+ \Delta t W^n \]](form_209.png)
The coefficients \form#210, \form#199, \form#211, \form#212 depend on \form#189 and \form#188. </li> </ol>
Definition at line 121 of file TimeAdvanceNewmark.hpp.
| typedef TimeAdvance< feVectorType > super |
Definition at line 130 of file TimeAdvanceNewmark.hpp.
| typedef super::feVector_Type feVector_Type |
Definition at line 132 of file TimeAdvanceNewmark.hpp.
Definition at line 134 of file TimeAdvanceNewmark.hpp.
Definition at line 137 of file TimeAdvanceNewmark.hpp.
| typedef feVectorContainerPtr_Type::iterator feVectorContainerPtrIterate_Type |
Definition at line 140 of file TimeAdvanceNewmark.hpp.
Definition at line 143 of file TimeAdvanceNewmark.hpp.
Empty Constructor.
Definition at line 303 of file TimeAdvanceNewmark.hpp.
|
inlinevirtual |
Destructor.
Definition at line 154 of file TimeAdvanceNewmark.hpp.
|
virtual |
Update the state vector.
Update the vectors of the previous time steps by shifting on the right the old values.
| solution | current (new) value of the state vector |
Implements TimeAdvance< feVectorType >.
Definition at line 311 of file TimeAdvanceNewmark.hpp.
| void RHSFirstDerivative | ( | const Real & | timeStep, |
| feVectorType & | rhsContribution | ||
| ) | const |
Update the right hand side 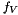 of the time derivative formula.
of the time derivative formula.
Return the right hand side 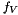 of the time derivative formula
of the time derivative formula
| timeStep | defined the time step need to compute the |
Definition at line 355 of file TimeAdvanceNewmark.hpp.
| void updateRHSSecondDerivative | ( | const Real & | timeStep = 1 | ) |
Update the right hand side 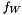 of the time derivative formula.
of the time derivative formula.
Set and Return the right hand side 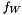 of the time derivative formula
of the time derivative formula
| timeStep | defined the time step need to compute the 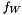 |
Definition at line 370 of file TimeAdvanceNewmark.hpp.
| void showMe | ( | std::ostream & | output = std::cout | ) | const |
Show the properties of temporal scheme.
Definition at line 386 of file TimeAdvanceNewmark.hpp.
Initialize the parameters of time advance scheme.
| order | define the order of BDF; |
| orderDerivatve | define the order of derivative; |
Definition at line 195 of file TimeAdvanceNewmark.hpp.
Initialize the parameters of time advance scheme.
| coefficients | define the TimeAdvanceNewmark's coefficients (, ); |
| orderDerivative | define the order of derivative; |
Definition at line 418 of file TimeAdvanceNewmark.hpp.
| void setInitialCondition | ( | const feVector_Type & | x0 | ) |
Initialize the StateVector.
Initialize all the entries of the unknown vector to be derived with the vector x0 (duplicated). this class is virtual because used in bdf;
| x0 | is the initial solution; |
Definition at line 509 of file TimeAdvanceNewmark.hpp.
| void setInitialCondition | ( | const feVector_Type & | x0, |
| const feVector_Type & | v0 | ||
| ) |
initialize the state vector
Initialize all the entries of the unknown vector to be derived with the vector x0, v0 (duplicated). this class is virtual because used in 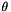 -method scheme;
-method scheme;
| x0 | is the initial unk; |
| v0 | is the initial velocity |
initialize zero
Definition at line 539 of file TimeAdvanceNewmark.hpp.
| void setInitialCondition | ( | const feVector_Type & | x0, |
| const feVector_Type & | v0, | ||
| const feVector_Type & | w0 | ||
| ) |
initialize the state vector
Initialize all the entries of the unknown vector to be derived with the vector x0, v0,w0 (duplicated). this class is virtual because used in Newamrk scheme;
| x0 | is the initial solution; |
| v0 | is the initial velocity |
| w0 | is the initial acceleration |
initialize zero
Definition at line 566 of file TimeAdvanceNewmark.hpp.
| void setInitialCondition | ( | const feVectorSharedPtrContainer_Type & | x0 | ) |
Initialize the state vector.
Initialize all the entries of the unknown vector to be derived with a set of vectors x0 note: this is taken as a copy (not a reference), since x0 is resized inside the method.
initialize zero
Definition at line 594 of file TimeAdvanceNewmark.hpp.
Return the 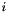 -th coefficient of the unk's extrapolation.
-th coefficient of the unk's extrapolation.
| i | index of extrapolation coefficient |
Definition at line 634 of file TimeAdvanceNewmark.hpp.
Return the 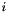 -th coefficient of the velocity's extrapolation.
-th coefficient of the velocity's extrapolation.
Definition at line 654 of file TimeAdvanceNewmark.hpp.
| void extrapolation | ( | feVector_Type & | extrapolation | ) | const |
Compute the polynomial extrapolation of solution.
Compute the polynomial extrapolation approximation of order  of
of 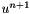 defined by the n stored state vectors
defined by the n stored state vectors
Definition at line 672 of file TimeAdvanceNewmark.hpp.
| void extrapolationFirstDerivative | ( | feVector_Type & | extrapolation | ) | const |
Compute the polynomial extrapolation of velocity.
Compute the polynomial extrapolation approximation of order  of
of 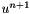 defined by the n stored state vectors
defined by the n stored state vectors
Definition at line 685 of file TimeAdvanceNewmark.hpp.
|
inline |
Return the current velocity.
Definition at line 276 of file TimeAdvanceNewmark.hpp.
|
inline |
Return the current acceleration.
Definition at line 282 of file TimeAdvanceNewmark.hpp.
|
private |
Coefficient of TimeAdvanceNewmark: 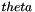 .
.
Definition at line 292 of file TimeAdvanceNewmark.hpp.
|
private |
Coefficient of TimeAdvanceNewmark: 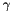 .
.
Definition at line 295 of file TimeAdvanceNewmark.hpp.