 |
LifeV
|
 |
LifeV
|
timeAdvance_template - File containing a class to deal the time advancing scheme More...
#include <TimeAdvance.hpp>
 Inheritance diagram for TimeAdvance< feVectorType >:
Inheritance diagram for TimeAdvance< feVectorType >:Public Types | |
| typedef feVectorType | feVector_Type |
| typedef ScalarVector | container_Type |
| typedef std::vector< feVector_Type > | feVectorContainer_Type |
| typedef std::vector< feVector_Type * > | feVectorContainerPtr_Type |
| typedef feVectorContainerPtr_Type::iterator | feVectorContainerPtrIterate_Type |
| typedef std::vector< std::shared_ptr< feVector_Type > > | feVectorSharedPtrContainer_Type |
Constructor & Destructor | |
| TimeAdvance () | |
| Empty Constructor. More... | |
| virtual | ~TimeAdvance () |
| Destructor. More... | |
Methods | |
| virtual void | shiftRight (const feVector_Type &solution)=0 |
| Update the vectors of the previous time steps by shifting on the right. More... | |
timeAdvance_template - File containing a class to deal the time advancing scheme
This class define an abstract method to build temporal discretization schemes. In particular we consider problems of the first order and the second order in time; that after space and time discretization, and suitable linearisation of non linear operator, we obtain a linear system to solve at each time step (or each iteration ):
![\[ K U^{n+1} =F^{n+1}\]](form_115.png)
where 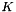 is an opportune matrix,
is an opportune matrix, 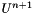 is the unknown vector and
is the unknown vector and 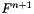 is the right hand side vector at the time
is the right hand side vector at the time 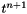 . To determine
. To determine 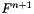 we define the state vector
we define the state vector 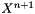 that contained the informations about previous solutions.
that contained the informations about previous solutions.
First order problems:
![\[ M \frac{\partial u}{\partial t} + L( u) = f ,\]](form_120.png)
where L is a generic nonlinear operator. We define U an approximation of u and the velocity vector 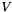 an approximation of
an approximation of 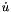 at the time step
at the time step 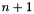 as
as
![\[ V^{n+1}=\frac{\alpha_0}{\Delta t} U^{n+1}- f_V^{n+1}, \]](form_124.png)
where 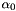 is a suitable coefficient and
is a suitable coefficient and 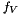 is a linear combination of the previous solutions
is a linear combination of the previous solutions 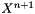 with coefficients
with coefficients 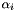 , that will be specified in the following.
, that will be specified in the following.
Then the time discrete version is
![\[ \frac{\alpha_0}{\Delta t}M U^{n+1} +A (U^{n+1})= f^{n+1}+ M f_V^{n+1} \]](form_128.png)
, that can be solved by any non-linear iterative solver (fixed point, Newton, ....). This class provides also a suitable extrapolation 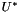 of
of 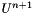 , given by a linear combination of previous solutions and of order consistent with the time discretization formula.
, given by a linear combination of previous solutions and of order consistent with the time discretization formula.
In this part we want to extend the previous approach to second order problems in time.
Second order problems:
![\[ \ddot{ u} + L( \dot{u}, u) = f \]](form_131.png)
where 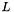 is non linear operator.
is non linear operator.
We consider the following semidiscrete problem
![\[ M \frac{d^2 U}{d t^2} + D ( U, \frac{d U}{d t} ) + A ( U ) = f \]](form_133.png)
where 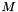 is the mass matrix,
is the mass matrix, 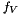 the forcing term and
the forcing term and 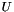 is the vector of unknowns.
is the vector of unknowns.
We define the following quantities
![\[ V :=\frac{d U}{d t }\qquad W := \frac{d^2 U} {d t^2}, \]](form_136.png)
where 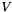 and
and 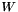 are the velocity and the acceleration vectors, respectively.
are the velocity and the acceleration vectors, respectively.
At the time step 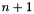 , we consider the following approximations of
, we consider the following approximations of 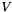 and
and 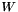 :
:
![\[ V^{n+1}=\frac{\alpha_0}{\Delta t} U^{n+1}- f_V^{n+1}, \]](form_124.png)
and
![\[ W^{n+1}=\frac{\xi_0}{\Delta t^2} U^{n+1} - f_W^{n+1}, \]](form_138.png)
where 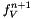 and
and 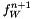 are linear combinations of the previous solutions with suitable coefficients
are linear combinations of the previous solutions with suitable coefficients 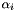 and
and 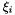 , respectively. If
, respectively. If 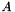 and
and 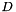 depend on
depend on 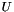 and
and 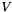 we can linearise the problem using suitable extrapolations
we can linearise the problem using suitable extrapolations 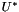
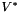 obtained by linear combinations of previous solutions with coefficients
obtained by linear combinations of previous solutions with coefficients 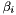 and
and 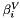 respectively.
respectively.
Definition at line 130 of file TimeAdvance.hpp.
| typedef feVectorType feVector_Type |
Definition at line 137 of file TimeAdvance.hpp.
| typedef ScalarVector container_Type |
Definition at line 140 of file TimeAdvance.hpp.
| typedef std::vector<feVector_Type> feVectorContainer_Type |
Definition at line 143 of file TimeAdvance.hpp.
| typedef std::vector<feVector_Type*> feVectorContainerPtr_Type |
Definition at line 146 of file TimeAdvance.hpp.
| typedef feVectorContainerPtr_Type::iterator feVectorContainerPtrIterate_Type |
Definition at line 149 of file TimeAdvance.hpp.
| typedef std::vector<std::shared_ptr<feVector_Type> > feVectorSharedPtrContainer_Type |
Definition at line 152 of file TimeAdvance.hpp.
| TimeAdvance | ( | ) |
Empty Constructor.
Definition at line 513 of file TimeAdvance.hpp.
|
virtual |
Destructor.
Definition at line 524 of file TimeAdvance.hpp.
|
pure virtual |
Update the vectors of the previous time steps by shifting on the right.
Update the vectors of the previous time steps by shifting on the right the old values.
| solution | is a (new) value of the state vector |
Implemented in TimeAdvanceBDF< feVectorType >, TimeAdvanceBDF< double >, TimeAdvanceBDF< VectorType >, TimeAdvanceBDF< vector_Type >, and TimeAdvanceNewmark< feVectorType >.