HyperbolicSolver Implements an hyperbolic solver. More...

#include <HyperbolicSolver.hpp>

Collaboration diagram for HyperbolicSolver< Mesh, SolverType >:

Protected Attributes
const UInt	M_me
	MPI process identifier. More...

MapEpetra	M_localMap
	Local map. More...

Displayer	M_displayer
	Parallel displayer. More...

const data_Type &	M_data
	Data for Darcy solvers. More...

Function_Type	M_source
	Source function. More...

Function_Type	M_mass
	Mass function, it does not depend on time. More...

bchandlerPtr_Type	M_BCh
	Bondary conditions handler. More...

bool	M_setBC
	Flag if the boundary conditions are setted or not. More...

Function_Type	M_initialSolution
	Function of initial solution. More...

fluxPtr_Type	M_numericalFlux
	Class of type AbstractNumericalFlux for local flux computations. More...

FESpace< Mesh, MapEpetra > &	M_FESpace
	Finite element space. More...

vectorPtr_Type	M_rhs
	Right hand side. More...

vectorPtr_Type	M_u
	Solution at current time step. More...

vectorPtr_Type	M_uOld
	Solution at previous time step. More...

vectorPtr_Type	M_globalFlux
	Computed numerical flux. More...

VectorElemental	M_localFlux
	Auxiliary vector for local fluxes. More...

std::vector< MatrixElemental >	M_elmatMass
	Vector of all local mass matrices, possibly with mass function. More...

Public Types
typedef std::function< Real(const Real &, const Real &, const Real &, const Real &, const UInt &) >	Function_Type

typedef HyperbolicData< Mesh >	data_Type

typedef BCHandler	bchandler_Type

typedef std::shared_ptr< bchandler_Type >	bchandlerPtr_Type

typedef SolverType::vector_type	vector_Type

typedef std::shared_ptr< vector_Type >	vectorPtr_Type

typedef Epetra_Comm	comm_Type

typedef std::shared_ptr< comm_Type >	commPtr_Type

typedef AbstractNumericalFlux< Mesh, SolverType >	flux_Type

typedef std::shared_ptr< flux_Type >	fluxPtr_Type

typedef Real	ghostData_Type

typedef std::vector< ghostData_Type >	ghostDataContainer_Type

typedef std::map< UInt, ghostDataContainer_Type >	buffer_Type

typedef std::map< ID, ghostData_Type >	ghostDataMap_Type

Constructors & Destructor
	HyperbolicSolver (const data_Type &dataFile, FESpace< Mesh, MapEpetra > &fESpace, MapEpetra &ghostMap, bchandler_Type &bcHandler, commPtr_Type &comm)
	Full constructor for the class. More...

	HyperbolicSolver (const data_Type &dataFile, FESpace< Mesh, MapEpetra > &fESpace, MapEpetra &ghostMap, commPtr_Type &comm)
	Constructor for the class without the definition of the boundary handler. More...

virtual	~HyperbolicSolver ()
	Virtual destructor. More...

Methods
void	setup ()
	Setup the local mass matrices. More...

void	solveOneTimeStep ()
	Solve one time step of the hyperbolic problem. More...

Real	CFL ()
	Compute the global CFL condition. More...

Set Methos
void	setInitialSolution (const Function_Type &initialSolution)
	Set the initial solution for the computation. More...

void	setBoundaryCondition (bchandler_Type &bcHandler)
	Set the boundary conditions. More...

void	setSourceTerm (const Function_Type &source)
	Set the source term. More...

void	setMassTerm (const Function_Type &mass)
	Set the mass function term. More...

void	setNumericalFlux (const flux_Type &flux)
	Set the numerical flux. More...

void	setSolution (const vectorPtr_Type &solution)
	Set the solution vector. More...

Get Methods
const vectorPtr_Type &	solution () const
	Returns the solution vector. More...

bool	isBoundaryConditionSet () const
	Return if the bounday conditions is setted or not. More...

bchandlerPtr_Type &	boundaryConditionHandler ()
	Return the boundary conditions handler. More...

MapEpetra const &	map () const
	Return the Epetra local map. More...

Displayer const &	getDisplayer () const
	Return the displayer. More...

Displayer &	getDisplayer ()
	Returns displayer. More...

Protected Methods
void	localReconstruct (const UInt &Elem)
	Reconstruct locally the solution. More...

void	localEvolve (const UInt &iElem)
	Compute the local contribute. More...

void	localAverage (const UInt &iElem)
	Apply the flux limiters locally. More...

Private Constructors
	HyperbolicSolver (const HyperbolicSolver< Mesh, SolverType > &)
	Inhibited copy constructor. More...

Private Operators
HyperbolicSolver &	operator= (const HyperbolicSolver< Mesh, SolverType > &)
	Inhibited assign operator. More...

Detailed Description

template<typename Mesh, typename SolverType = LifeV::SolverAztecOO>
class LifeV::HyperbolicSolver< Mesh, SolverType >

HyperbolicSolver Implements an hyperbolic solver.

Author: Alessio Fumagalli aless.nosp@m.io.f.nosp@m.umaga.nosp@m.lli@.nosp@m.mail..nosp@m.poli.nosp@m.mi.it; Michel Kern miche.nosp@m.l.ke.nosp@m.rn@in.nosp@m.ria..nosp@m.fr

See also: For applications related to two-phase flow see [8]

This class implements an hyperbolic solver.

This class solves a general hyperbolic scalar equation in the conservative form: find 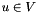$u \in V$ such that

$\left\{ \begin{array}{l l} \displaystyle \frac{\partial u}{\partial t} + \nabla \cdot \mathbf{F} ( u ) = f & \mathrm{ in } \quad \Omega \times [0,T]\,, \\ u(\mathbf{x}, 0) = u_0( \mathbf{x} ) & \mathrm{ in } \quad \Omega\,, \end{array} \right.$

with prescribed inflow boundary conditions on 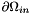$\partial \Omega_{in}$

$u = \bar{u} \quad \mathrm{ on } \quad \partial \Omega_{in}\,.$

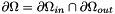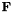We have $\partial \Omega = \partial \Omega_{in} \cap \partial \Omega_{out}$ . Since this solver can be used coupled with an elliptic solver, the Neumann and Robin boundary are trated as outflow boundary, while the Dirichlet boundary is automatically dedived into outflow boundary and inflow boundary. This choice is due to the general form of the flux function $\mathbf{F}$ .
Introducing a conforming triangolation 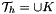$\mathcal{T}_h = \cup K$ of the domain 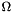$\Omega$ , we write the strong formulation in a weak form in each element 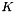$ K $ : give a test function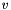 $ v $

$\displaystyle \int_K \frac{\partial u}{\partial t} v + \int_K \nabla \cdot \mathbf{F} ( u ) v = \int_K f v \quad \forall v \in V\,,$

integrating by part the integral with the divergence we find

$\displaystyle \int_K \frac{\partial u}{\partial t} v - \int_K \mathbf{F} ( u ) \cdot \nabla v + \int_{\partial K} \mathbf{F}( u ) \cdot \mathbf{n} v = \int_K f v \quad \forall v \in V\,.$

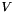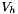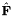The Discontinuous Galerkin formulation of the problem is given approximating $ V $ with a discontinuous finite element space $ V_h $ , while the numerical flux at the boundaries is approximated using a suitable numerical scheme obtaining $\hat{\mathbf{F}}$ .
Summing on all the elements 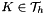$K \in \mathcal{T}_h$ , the finite element problem reads: find 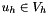$u_h \in V_h$ such that

$\displaystyle \sum_{K \in \mathcal{T}_h} \int_K \frac{\partial u_h}{\partial t} v_h - \int_K \mathbf{F} ( u_h ) \cdot \nabla v_h + \int_{\partial K} \hat{\mathbf{F}}( u_h ) \cdot \mathbf{n} v_h = \sum_{K \in \mathcal{T}_h} \int_K f v_h \quad \forall v_h \in V_h\,.$

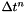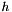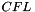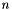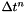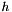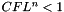Each time step $\Delta t^n$ and mesh size $ h $ are coupled via $ CFL $ condition at step $ n $ , using esplicit Euler scheme we find the relation between $\Delta t^n$ and $ h $ satysfying $ CFL^n < 1 $ .
A general form for computing the 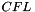$ CFL $ condition is

$CFL^n = \displaystyle \sup_{e \in \partial K, K \in \mathcal{T}_h } \Delta t^n \frac{\vert e \vert}{ \vert K \vert } \Vert \mathbf{F}^\prime \cdot \mathbf{n}_{e, K} \Vert_{L^\infty(a_0, b_0) }\,,$

where

$\begin{array}{l} \displaystyle a_0 = \inf_{x \in \Omega, t \in (t^{n-1}, t^n), y \in \partial \Omega_{in} } \left\{ u_0, \bar{u}(y, t) \right\}\,, \\ \displaystyle b_0 = \sup_{x \in \Omega, t \in (t^{n-1}, t^n), y \in \partial \Omega_{in} } \left\{ u_0, \bar{u}(y, t) \right\}\,. \end{array}$

Local approximation for the flux function 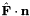$\hat{\mathbf{F}} \cdot \mathbf{n}$ and the computation of 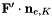$\mathbf{F}^\prime \cdot \mathbf{n}_{e, K}$ are in NumericalFlux.hpp file.

Note: The implementation is given just for lowest order discontinuous finite elements.

Todo:

Implement the forcing term 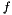$ f $ and implement high order finite elements.

When we will pass to Trilinos >= 10.6 use Epetra wrapper for LAPACK functions.

Definition at line 122 of file HyperbolicSolver.hpp.

Member Typedef Documentation

◆ Function_Type

typedef std::function< Real ( const Real&, const Real&, const Real&, const Real&, const UInt& ) > Function_Type

Definition at line 132 of file HyperbolicSolver.hpp.

◆ data_Type

typedef HyperbolicData< Mesh > data_Type

Definition at line 134 of file HyperbolicSolver.hpp.

◆ bchandler_Type

typedef BCHandler bchandler_Type

Definition at line 136 of file HyperbolicSolver.hpp.

◆ bchandlerPtr_Type

typedef std::shared_ptr< bchandler_Type > bchandlerPtr_Type

Definition at line 137 of file HyperbolicSolver.hpp.

◆ vector_Type

typedef SolverType::vector_type vector_Type

Definition at line 139 of file HyperbolicSolver.hpp.

◆ vectorPtr_Type

typedef std::shared_ptr< vector_Type > vectorPtr_Type

Definition at line 140 of file HyperbolicSolver.hpp.

◆ comm_Type

typedef Epetra_Comm comm_Type

Definition at line 142 of file HyperbolicSolver.hpp.

◆ commPtr_Type

typedef std::shared_ptr< comm_Type > commPtr_Type

Definition at line 143 of file HyperbolicSolver.hpp.

◆ flux_Type

typedef AbstractNumericalFlux<Mesh, SolverType> flux_Type

Definition at line 145 of file HyperbolicSolver.hpp.

◆ fluxPtr_Type

typedef std::shared_ptr< flux_Type > fluxPtr_Type

Definition at line 146 of file HyperbolicSolver.hpp.

◆ ghostData_Type

typedef Real ghostData_Type

Definition at line 148 of file HyperbolicSolver.hpp.

◆ ghostDataContainer_Type

typedef std::vector< ghostData_Type > ghostDataContainer_Type

Definition at line 149 of file HyperbolicSolver.hpp.

◆ buffer_Type

typedef std::map< UInt, ghostDataContainer_Type > buffer_Type

Definition at line 150 of file HyperbolicSolver.hpp.

◆ ghostDataMap_Type

typedef std::map< ID, ghostData_Type > ghostDataMap_Type

Definition at line 151 of file HyperbolicSolver.hpp.

Constructor & Destructor Documentation

◆ HyperbolicSolver() [1/3]

HyperbolicSolver	(	const data_Type &	dataFile,
		FESpace< Mesh, MapEpetra > &	fESpace,
		MapEpetra &	ghostMap,
		bchandler_Type &	bcHandler,
		commPtr_Type &	comm
	)

Full constructor for the class.

Parameters

dataFile	Data for the problem.
fESpace	Discontinuous finite element space.
bcHandler	Boundary conditions for the problem.
comm	Shared pointer of the Epetra communicator.

Definition at line 421 of file HyperbolicSolver.hpp.

Here is the caller graph for this function:

◆ HyperbolicSolver() [2/3]

HyperbolicSolver	(	const data_Type &	dataFile,
		FESpace< Mesh, MapEpetra > &	fESpace,
		MapEpetra &	ghostMap,
		commPtr_Type &	comm
	)

Constructor for the class without the definition of the boundary handler.

Parameters

dataFile	Data for the problem.
fESpace	Discontinuous finite element space.
comm	Shared pointer of the Epetra communicator.

Definition at line 458 of file HyperbolicSolver.hpp.

Here is the caller graph for this function:

◆ ~HyperbolicSolver()

~HyperbolicSolver ( )

virtual

Virtual destructor.

Definition at line 493 of file HyperbolicSolver.hpp.

◆ HyperbolicSolver() [3/3]

HyperbolicSolver ( const HyperbolicSolver< Mesh, SolverType > & )

private

Inhibited copy constructor.

Member Function Documentation

◆ setup()

void setup ( )

Setup the local mass matrices.

Definition at line 506 of file HyperbolicSolver.hpp.

◆ solveOneTimeStep()

void solveOneTimeStep ( )

Solve one time step of the hyperbolic problem.

Definition at line 575 of file HyperbolicSolver.hpp.

◆ CFL()

Real CFL ( )

Compute the global CFL condition.

Definition at line 629 of file HyperbolicSolver.hpp.

◆ setInitialSolution()

void setInitialSolution ( const Function_Type & initialSolution )

Set the initial solution for the computation.

Compute the initial solution as an interpolation on the analytical initial solution.

Parameters

initialSolution The initial solution function.

Definition at line 760 of file HyperbolicSolver.hpp.

◆ setBoundaryCondition()

void setBoundaryCondition ( bchandler_Type & bcHandler )

inline

Set the boundary conditions.

Parameters

bcHandler Boundary condition handler for the problem.

Definition at line 216 of file HyperbolicSolver.hpp.

◆ setSourceTerm()

void setSourceTerm ( const Function_Type & source )

inline

Set the source term.

Definition at line 227 of file HyperbolicSolver.hpp.

◆ setMassTerm()

void setMassTerm ( const Function_Type & mass )

inline

Set the mass function term.

It does not depend on time. The default setted source term is 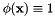$\phi( \mathbf{x} ) \equiv 1$ .

Parameters

mass	Mass term for the problem.

Definition at line 237 of file HyperbolicSolver.hpp.

◆ setNumericalFlux()

void setNumericalFlux ( const flux_Type & flux )

inline

Set the numerical flux.

Parameters

flux	The numerical flux class

Definition at line 246 of file HyperbolicSolver.hpp.

◆ setSolution()

void setSolution ( const vectorPtr_Type & solution )

inline

Set the solution vector.

Parameters

solution Constant vector_type reference of the solution.

Definition at line 256 of file HyperbolicSolver.hpp.

◆ solution()

const vectorPtr_Type& solution ( ) const

inline

Returns the solution vector.

Returns: Constant vector_type reference of the solution vector.

Definition at line 272 of file HyperbolicSolver.hpp.

◆ isBoundaryConditionSet()

bool isBoundaryConditionSet ( ) const

inline

Return if the bounday conditions is setted or not.

Returns: Constant boolean with value true if the boundary condition is setted, false otherwise

Definition at line 282 of file HyperbolicSolver.hpp.

◆ boundaryConditionHandler()

bchandlerPtr_Type& boundaryConditionHandler ( )

inline

Return the boundary conditions handler.

Returns: Reference of boundary conditions handler.

Definition at line 291 of file HyperbolicSolver.hpp.

◆ map()

MapEpetra const& map ( ) const

inline

Return the Epetra local map.

Returns: Constant MapEpetra reference of the problem.

Definition at line 301 of file HyperbolicSolver.hpp.

◆ getDisplayer() [1/2]

Displayer const& getDisplayer ( ) const

inline

Return the displayer.

Useful for parallel print in programs.

Returns: Constant reference of the displayer of the problem.

Definition at line 311 of file HyperbolicSolver.hpp.

◆ getDisplayer() [2/2]

Displayer& getDisplayer ( )

inline

Returns displayer.

Returns: Reference of the displayer of the problem.

Definition at line 320 of file HyperbolicSolver.hpp.

◆ localReconstruct()

void localReconstruct ( const UInt & Elem )

protected

Reconstruct locally the solution.

Definition at line 784 of file HyperbolicSolver.hpp.

Here is the caller graph for this function:

◆ localEvolve()

void localEvolve ( const UInt & iElem )

protected

Compute the local contribute.

Definition at line 795 of file HyperbolicSolver.hpp.

Here is the caller graph for this function:

◆ localAverage()

void localAverage ( const UInt & iElem )

protected

Apply the flux limiters locally.

Definition at line 998 of file HyperbolicSolver.hpp.

Here is the caller graph for this function:

◆ operator=()

HyperbolicSolver& operator= ( const HyperbolicSolver< Mesh, SolverType > & )

private

Inhibited assign operator.

Field Documentation

◆ M_me

const UInt M_me

protected

MPI process identifier.

Definition at line 344 of file HyperbolicSolver.hpp.

◆ M_localMap

MapEpetra M_localMap

protected

Local map.

Definition at line 347 of file HyperbolicSolver.hpp.

◆ M_displayer

Displayer M_displayer

protected

Parallel displayer.

Definition at line 350 of file HyperbolicSolver.hpp.

◆ M_data

const data_Type& M_data

protected

Data for Darcy solvers.

Definition at line 353 of file HyperbolicSolver.hpp.

◆ M_source

Function_Type M_source

protected

Source function.

Definition at line 356 of file HyperbolicSolver.hpp.

◆ M_mass

Function_Type M_mass

protected

Mass function, it does not depend on time.

Definition at line 359 of file HyperbolicSolver.hpp.

◆ M_BCh

bchandlerPtr_Type M_BCh

protected

Bondary conditions handler.

Definition at line 362 of file HyperbolicSolver.hpp.

◆ M_setBC

bool M_setBC

protected

Flag if the boundary conditions are setted or not.

Definition at line 365 of file HyperbolicSolver.hpp.

◆ M_initialSolution

Function_Type M_initialSolution

protected

Function of initial solution.

Definition at line 368 of file HyperbolicSolver.hpp.

◆ M_numericalFlux

fluxPtr_Type M_numericalFlux

protected

Class of type AbstractNumericalFlux for local flux computations.

Definition at line 371 of file HyperbolicSolver.hpp.

◆ M_FESpace

FESpace<Mesh, MapEpetra>& M_FESpace

protected

Finite element space.

Definition at line 374 of file HyperbolicSolver.hpp.

◆ M_rhs

vectorPtr_Type M_rhs

protected

Right hand side.

Definition at line 377 of file HyperbolicSolver.hpp.

◆ M_u

vectorPtr_Type M_u

protected

Solution at current time step.

Definition at line 380 of file HyperbolicSolver.hpp.

◆ M_uOld

vectorPtr_Type M_uOld

protected

Solution at previous time step.

Definition at line 383 of file HyperbolicSolver.hpp.

◆ M_globalFlux

vectorPtr_Type M_globalFlux

protected

Computed numerical flux.

Definition at line 386 of file HyperbolicSolver.hpp.

◆ M_localFlux

VectorElemental M_localFlux

protected

Auxiliary vector for local fluxes.

Definition at line 389 of file HyperbolicSolver.hpp.

◆ M_elmatMass

std::vector<MatrixElemental> M_elmatMass

protected

Vector of all local mass matrices, possibly with mass function.

Definition at line 392 of file HyperbolicSolver.hpp.

The documentation for this class was generated from the following file:

HyperbolicSolver.hpp

Protected Attributes

Public Types

Constructors & Destructor

Methods

Set Methos

Get Methods

Protected Methods

Private Constructors

Private Operators

Detailed Description

template<typename Mesh, typename SolverType = LifeV::SolverAztecOO> class LifeV::HyperbolicSolver< Mesh, SolverType >

Member Typedef Documentation

◆ Function_Type

◆ data_Type

◆ bchandler_Type

◆ bchandlerPtr_Type

◆ vector_Type

◆ vectorPtr_Type

◆ comm_Type

◆ commPtr_Type

◆ flux_Type

◆ fluxPtr_Type

◆ ghostData_Type

◆ ghostDataContainer_Type

◆ buffer_Type

◆ ghostDataMap_Type

Constructor & Destructor Documentation

◆ HyperbolicSolver() [1/3]

◆ HyperbolicSolver() [2/3]

◆ ~HyperbolicSolver()

◆ HyperbolicSolver() [3/3]

Member Function Documentation

◆ setup()

◆ solveOneTimeStep()

◆ CFL()

◆ setInitialSolution()

◆ setBoundaryCondition()

◆ setSourceTerm()

◆ setMassTerm()

◆ setNumericalFlux()

◆ setSolution()

◆ solution()

◆ isBoundaryConditionSet()

◆ boundaryConditionHandler()

◆ map()

◆ getDisplayer() [1/2]

◆ getDisplayer() [2/2]

◆ localReconstruct()

◆ localEvolve()

◆ localAverage()

◆ operator=()

Field Documentation

◆ M_me

◆ M_localMap

◆ M_displayer

◆ M_data

◆ M_source

◆ M_mass

◆ M_BCh

◆ M_setBC

◆ M_initialSolution

◆ M_numericalFlux

◆ M_FESpace

◆ M_rhs

◆ M_u

◆ M_uOld

◆ M_globalFlux

◆ M_localFlux

◆ M_elmatMass

template<typename Mesh, typename SolverType = LifeV::SolverAztecOO>
class LifeV::HyperbolicSolver< Mesh, SolverType >