Special routines to read meshes and special structures for sides and faces handling. More...

#include <utility>
#include <algorithm>
#include <lifev/core/LifeV.hpp>
#include <lifev/core/mesh/ElementShapes.hpp>

Include dependency graph for MeshElementBare.hpp:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Data Structures
struct	BareVertex
	The Vertex basis class. More...

struct	BareEdge
	The Edge basis class. More...

struct	BareFace
	The base Face class. More...

struct	cmpBareItem< T >
	General functor for lexicographic comparison. More...

struct	cmpBareItem< BareVertex >
	Specialized functor for Vertices. More...

struct	cmpBareItem< BareEdge >
	Specialized functor for Edges. More...

struct	cmpBareItem< BareFace >
	Specialized functor for Faces. More...

class	BareEntitySelector< Shape >
	BareEntitySelector class - Select the proper bare entity type (bareEdge or bareFace) based on the number of the entity points. More...

struct	BareEntitySelector< Point >

struct	BareEntitySelector< Line >

struct	BareEntitySelector< Triangle >

struct	BareEntitySelector< Quad >

class	MeshElementBareHandler< BareItemType >
	MeshElementBareHandler class - Class to handle bare edges and faces construction. More...

Namespaces
	LifeV
	Default Physical Solver.

Functions
std::pair< BareEdge, bool >	makeBareEdge (ID const i, ID const j)
	It creates a BareEdge end returns the orientation of the created edge with respect to the given data. More...

BareEdge	setBareEdge (ID const i, ID const j)
	It creates a BareEdge, ignoring orientation. More...

BareEdge	setBareEdgeNo (ID const i, ID const j)
	It creates a non-standard BareEdge. More...

std::pair< BareFace, bool >	makeBareFace (ID const i, ID const j, ID const k)
	It creates Bare Face objects from three Point ID's. More...

std::pair< BareFace, bool >	makeBareFace (ID const i, ID const j, ID const k, ID const l)
	It creates Bare Face objects from four Point ID's. To be used with Quad faces. More...

bool	operator!= (const BareEdge &edge1, const BareEdge &edge2)
	inequality More...

bool	operator== (const BareEdge &edge1, const BareEdge &edge2)
	equality More...

bool	operator> (const BareEdge &edge1, const BareEdge &edge2)
	greater than More...

bool	operator>= (const BareEdge &edge1, const BareEdge &edge2)
	greater-equal than More...

bool	operator< (const BareEdge &edge1, const BareEdge &edge2)
	less than More...

bool	operator<= (const BareEdge &edge1, const BareEdge &edge2)
	less-equal than More...

bool	operator!= (const BareFace &face1, const BareFace &face2)
	inequality More...

bool	operator== (const BareFace &face1, const BareFace &face2)
	equality More...

bool	operator< (const BareFace &f1, const BareFace &f2)

Detailed Description

Special routines to read meshes and special structures for sides and faces handling.

Classes BareFace and BareEdge have been created to give an UNIQUE Representation for mesh faces and edges and thus allow the construction of global tables or fields.

Author: Luca Formaggia luca..nosp@m.form.nosp@m.aggia.nosp@m.@pol.nosp@m.imi.i.nosp@m.t

Contributor:: Luca Bertagna lbert.nosp@m.ag@e.nosp@m.mory..nosp@m.edu

Contributor:: Lucia Mirabella lucia.nosp@m..mir.nosp@m.abell.nosp@m.@gma.nosp@m.il.co.nosp@m.m

Maintainer:: Lucia Mirabella lucia.nosp@m..mir.nosp@m.abell.nosp@m.@gma.nosp@m.il.co.nosp@m.m

Date: 19-08-1999

Classes BareFace and BareEdge have been created to give an UNIQUE internal representation for mesh faces and edges, allowing thus the construction of DOF objects (which are naturally linked to mesh entities).

Introduction

One of the paradigms chosen for the development of this library is the fact that degrees of freedom (DOF) are linked to geometrical entities. Now if we have degrees of freedom associated, for instance, to an Edge (like in a P2 Tetra) in order to build the global numbering of the DOF and the association between local (element-wise) and global numbering, we need to identify edges and give them a unique ID. Yet, we may not want to build a full Edge (MeshElementMarked2D) object: we only need the ID of the edge and a way of computing the ID's of the degrees of freedom on the edge, all the remaining data of a full Edge object is not necessarily needed.

Another related problem is how to uniquely identify a face or an edge in the mesh.

The dilemma has been resolved by creating the concept of a BareEdge and BareFace (bare geometry items). A bare geometry item is formed by the minimal information required to uniquely identify it, namely 2 Point's ID 's for an edge and 3 Point's ID 's for the Faces (it is enough also for Quad faces!). We build the bare items by looping through the elements and obviously we make sure that the BareItem ID is consistent with that of the corresponding ``full item'' if the latter has been instantiated.

Another very important issue is that of orientation. There are different ways of considering orientation of a Face or an Edge. The first is the local orientation of a Face or Edge of the reference finite element. This is conventionally chosen when designing the finite elements. For the faces, we have adopted the convention that the local positive orientation is such that the face normal calculated with the right hand rule is outwardly oriented. As for the edges, the local orientation for a 3D element is more arbitrary.

However, for a 2D element, the positive orientation of an Edge is the one which is in accordance with the right hand rule applied to that element.

When a Face or an edge is active, i.e. is effectively stored in the mesh, then there is another obvious orientation, of global rather than local nature: that induced by the way the edge or face is stored. For boundary elements (faced in 3D or edges in 2D) it is compulsory that the orientation of the stored item be consistent with the convention chosen for the orientation of the domain boundary. More precisely, boundary elements are stored so that the normal (always calculated following the right hand rule) is outward with respect to the domain.

However, there is the need of defining a global orientation also for non active entities. This because we do not always store all faces and all edges. We need then to choose a unique way to identify the orientation of an Edge or of a Face independently from the fact that they are active or not. We will call this orientation the natural orientation. We have chosen the following convention for natural orientation of faces and edges

The positive natural orientation of an Edge is given by 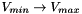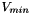$V_{min} \rightarrow V_{max}$ , $V_{min}$ being the Edge Vertex with smallest ID
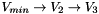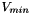The positive natural orientation of a Face is given by the cicle $V_{min} \rightarrow V_2\rightarrow V_3$ , $V_{min}$ being the Face Vertex with smallest ID, 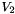the second smallest and 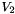the thirsd smallest.

Note that the latter definition applies both to triangular and to quad faces.

Warning: If I want to associate boundary conditions I need the active entity, since BareEdges do not store Marker data. (This is why the RegionMesh classes treat boundary items in a rather special way).

Definition in file MeshElementBare.hpp.

Data Structures

Namespaces

Functions

Detailed Description