 |
LifeV
|
 |
LifeV
|
Functions | |
| void | mass (MatrixElemental &localMass, const CurrentFE &massCFE, const Real &coefficient, const UInt &fieldDim) |
| Elementary mass for constant mass coefficient. More... | |
| void | stiffness (MatrixElemental &localStiff, const CurrentFE &stiffCFE, const Real &coefficient, const UInt &fieldDim) |
| Elementary stiffness for constant coefficient. More... | |
| void | advectionNewton (Real coef, VectorElemental &vel, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock) |
Assemble the term 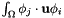 . More... . More... | |
| void | grad (MatrixElemental &elmat, const CurrentFE &uCFE, const CurrentFE &pCFE, const UInt &fieldDim) |
| void | divergence (MatrixElemental &elmat, const CurrentFE &uCFE, const CurrentFE &pCFE, const UInt &fieldDim, const Real &coefficient) |
| void | stiffStrain (MatrixElemental &localStiff, const CurrentFE &stiffCFE, const Real &coefficient, const UInt &fieldDim) |
| void | bodyForces (VectorElemental &localForce, const CurrentFE &massRhsCFE, const function_Type &fun, const Real &t, const UInt &fieldDim) |
| void | stiff_sd (Real coef, const VectorElemental &vec_loc, MatrixElemental &elmat, const CurrentFE &fe, const CurrentFE &fe2, int iblock=0, int jblock=0, int nb=1) |
| StreamLine Diffusion. More... | |
| void | grad (const int icoor, const VectorElemental &vec_loc, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, int iblock, int jblock) |
| Convective term with a local vector coefficient (useful for Navier-Stokes problem) More... | |
| void | grad_ss (const int icoor, const VectorElemental &vec_loc, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, int iblock=0, int jblock=0) |
| Convective term with a local vector coefficient for Navier-Stokes problem in Skew-Symmetric form. More... | |
| void | grad (const int icoor, const VectorElemental &vec_loc, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, const CurrentFE &fe3, int iblock=0, int jblock=0) |
| Convective term with a local vector coefficient (useful for Navier-Stokes problem+adv-diff) More... | |
| void | grad (const int &icoor, const std::vector< Real > &localVector, MatrixElemental &elmat, const CurrentFE ¤tFE1, const CurrentFE ¤tFE2, const int &iblock=0, const int &jblock=0) |
| Conective term with a local vector given by quadrature node. More... | |
| void | source (Real coef, VectorElemental &f, VectorElemental &elvec, const CurrentFE &fe, int fblock, int eblock) |
| void | source_fhn (Real coef_f, Real coef_a, VectorElemental &u, VectorElemental &elvec, const CurrentFE &fe, int fblock, int eblock) |
| void | source_advection (const Real &coefficient, const VectorElemental &beta_loc, const VectorElemental &uk_loc, VectorElemental &elvec, const CurrentFE &fe) |
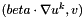 More... More... | |
| template<typename localVector > | |
| void | weightedMass (MatrixElemental &localMass, const CurrentFE &massCFE, const Real &coefficient, const localVector &localValues, const UInt &fieldDim) |
| Elementary weighted mass for constant mass coefficient. More... | |
| template<typename localVector , typename globalVector > | |
| void | interpolate (localVector &localValues, const CurrentFE &interpCFE, const UInt &spaceDim, const DOF &betaDof, const UInt &elementID, const globalVector &beta) |
| Interpolation procedure. More... | |
| template<typename localVector , typename globalVector > | |
| void | interpolateGradient (localVector &localGradient, const CurrentFE &interpCFE, const UInt &spaceDim, const DOF &betaDof, const UInt &elementID, const globalVector &beta) |
| Interpolation of the gradient. More... | |
| template<typename localVector , typename globalVector > | |
| void | interpolateDivergence (localVector &localDivergence, const CurrentFE &interpCFE, const DOF &betaDof, const UInt &elementID, const globalVector &beta) |
| Interpolation of the divergence. More... | |
| template<typename localVector > | |
| void | massDivW (MatrixElemental &localMass, const CurrentFE &massCFE, const Real &coefficient, const localVector &localValues, const UInt &fieldDim) |
| template<typename localVector > | |
| void | advection (MatrixElemental &localAdv, const CurrentFE &advCFE, const Real &coefficient, const localVector &localValues, const UInt &fieldDim) |
| Elementary advection u v. More... | |
| template<typename localTensor > | |
| void | symmetrizedAdvection (MatrixElemental &localAdv, const CurrentFE &advCFE, const Real &coefficient, const localTensor &localGradient, const UInt &fieldDim) |
| Elementary advection, term u v. More... | |
| template<typename UsrFct > | |
| void | source (const UsrFct &fct, VectorElemental &elvec, const CurrentFE &fe, int iblock=0) |
source 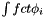 More... More... | |
| template<typename UsrFct > | |
| void | source (const UsrFct &fct, VectorElemental &elvec, const CurrentFE &fe, Real t, int iblock=0) |
source 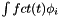 More... More... | |
Public typedefs | |
| typedef std::function< const Real(const Real &, const Real &, const Real &, const Real &, const ID &) > | function_Type |
| Use the portable syntax of the boost function. More... | |
Operators for classical finite elements | |
| void | mass (Real coef, MatrixElemental &elmat, const CurrentFE &fe, int iblock=0, int jblock=0) |
| coef(t,x,y,z,u) More... | |
| void | mass (Real coef, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, UInt nb) |
| void | mass (const std::vector< Real > &qpt_coef, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, UInt nb) |
| Mass term with coefficients given for each quadrature point. More... | |
| void | stiff_divgrad (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_divgrad_2 (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_gradgrad (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_gradgrad_2 (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_dergrad_gradbis (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_dergrad_gradbis_Tr (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_dergrad_gradbis_2 (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_dergrad_gradbis_Tr_2 (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_gradgradTr_gradbis (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_gradgradTr_gradbis_2 (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff_gradgradTr_gradbis_3 (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
| void | stiff (Real coef, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock) |
| void | stiff (Real coef, Real(*fct)(Real, Real, Real), MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock) |
| void | stiff (Real coef, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, int nb) |
| void | stiff (const std::vector< Real > &qpt_coef, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, int nb) |
| Stiff term with coefficient given for each quadrature node. More... | |
| void | stiff_curl (Real coef, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, int) |
| void | stiff_div (Real coef, MatrixElemental &elmat, const CurrentFE &fe) |
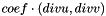 More... More... | |
| void | stiff_dergradbis (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
![$ coef \cdot ( [\nabla u^k]^T \nabla u : \nabla v )$](form_18.png) More... More... | |
| void | stiff_dergrad (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
![$ coef \cdot ( [\nabla u]^T \nabla u^k + [\nabla u^k]^T \nabla u : \nabla v )$](form_19.png) for Newton on St-Venant More... for Newton on St-Venant More... | |
| void | stiff_derdiv (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe) |
![$ coef \cdot ( trace { [\nabla u^k]^T \nabla u }, \nabla\cdot v ) $](form_20.png) for Newton on St-Venant More... for Newton on St-Venant More... | |
| void | stiff_strain (Real coef, MatrixElemental &elmat, const CurrentFE &fe) |
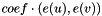 More... More... | |
| void | grad (const int icoor, Real coef, MatrixElemental &elmat, const CurrentFE &fe_u, const CurrentFE &fe_p, int iblock, int jblock) |
| void | div (const int icoor, Real coef, MatrixElemental &elmat, const CurrentFE &fe_u, const CurrentFE &fe_p, int iblock, int jblock) |
| void | grad_div (Real coef_grad, Real coef_div, MatrixElemental &elmat, const CurrentFE &fe_u, const CurrentFE &fe_p, int block_pres) |
| void | stab_stokes (Real visc, Real coef_stab, MatrixElemental &elmat, const CurrentFE &fe, int block_pres) |
| void | advection (Real coef, VectorElemental &vel, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, int nb) |
| void | source (Real constant, VectorElemental &elvec, const CurrentFE &fe, int iblock) |
| void | source_mass (const std::vector< Real > &constant, VectorElemental &elvec, const CurrentFE ¤tFe, const int &iblock) |
Assembly for the source term 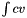 where where 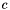 is a given by the values in the quadrature nodes. More... is a given by the values in the quadrature nodes. More... | |
| void | source_stiff (const std::vector< Real > &constant, VectorElemental &elvec, const CurrentFE ¤tFe, const int &iblock) |
Assembly for the source term 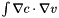 where where 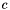 is a given by the values in the quadrature nodes. More... is a given by the values in the quadrature nodes. More... | |
| void | source_divuq (Real alpha, VectorElemental &uLoc, VectorElemental &elvec, const CurrentFE &fe_u, const CurrentFE &fe_p, int iblock) |
| void | source_gradpv (Real alpha, VectorElemental &pLoc, VectorElemental &elvec, const CurrentFE &fe_p, const CurrentFE &fe_u, int iblock) |
| template<typename UsrFct > | |
| void | advection (Real coef, const UsrFct &beta, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, int nb, Real t=0.) |
| void | source (Real constant, VectorElemental &elvec, const CurrentFE &fe, Real t, int iblock) |
Elementary operations for the interior penalty stabilization | |
| void | ipstab_grad (const Real coef, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, const CurrentFEManifold &bdfe, int iblock=0, int jblock=0) |
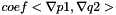 More... More... | |
| void | ipstab_grad (const Real coef, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, const CurrentFEManifold &bdfe, int iblock, int jblock, int nb) |
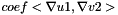 More... More... | |
| void | ipstab_bgrad (const Real coef, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, const VectorElemental &beta, const CurrentFEManifold &bdfe, int iblock, int jblock, int nb) |
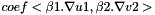 More... More... | |
| void | ipstab_div (const Real coef, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, const CurrentFEManifold &bdfe, int iblock=0, int jblock=0) |
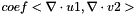 More... More... | |
| void | ipstab_bagrad (const Real coef, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, const VectorElemental &beta, const CurrentFEManifold &bdfe, int iblock=0, int jblock=0) |
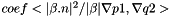 More... More... | |
| void | ipstab_bagrad (const Real coef, MatrixElemental &elmat, const CurrentFE &fe1, const CurrentFE &fe2, const CurrentFE &fe3, const VectorElemental &beta, const CurrentFEManifold &bdfe, int iblock=0, int jblock=0) |
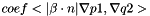 p1 lives in fe1 q2 lives in fe2 beta lives in fe3 More... p1 lives in fe1 q2 lives in fe2 beta lives in fe3 More... | |
Shape derivative terms for Newton FSI | |
| void | source_mass1 (Real coef, const VectorElemental &uk_loc, const VectorElemental &wk_loc, const VectorElemental &convect_loc, const VectorElemental &d_loc, VectorElemental &elvec, const CurrentFE &fe) |
![$ coef \cdot ( \nabla (-w^k):[I\nabla\cdot d - (\nabla d)^T] u^k + convect^T[I\nabla\cdot d - (\nabla d)^T] (\nabla u^k)^T , v ) $](form_34.png) for Newton FSI More... for Newton FSI More... | |
| void | source_mass2 (Real coef, const VectorElemental &uk_loc, const VectorElemental &dw_loc, VectorElemental &elvec, const CurrentFE &fe) |
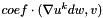 for Newton FSI More... for Newton FSI More... | |
| void | source_mass3 (Real coef, const VectorElemental &un_loc, const VectorElemental &uk_loc, const VectorElemental &d_loc, VectorElemental &elvec, const CurrentFE &fe) |
| void | source_stress (Real coef, Real mu, const VectorElemental &uk_loc, const VectorElemental &pk_loc, const VectorElemental &d_loc, VectorElemental &elvec, const CurrentFE &fe_u, const CurrentFE &fe_p) |
![$coef \cdot ( [-p^k I + 2\mu e(u^k)] [I\nabla\cdot d - (\nabla d)^T] , \nabla v )$](form_37.png) for Newton FSI More... for Newton FSI More... | |
| void | source_stress2 (Real coef, const VectorElemental &uk_loc, const VectorElemental &d_loc, VectorElemental &elvec, const CurrentFE &fe_u) |
![$+ \mu ( \nabla u^k \nabla d + [\nabla d]^T[\nabla u^k]^T : \nabla v )$](form_38.png) More... More... | |
| void | source_press (Real coef, const VectorElemental &uk_loc, const VectorElemental &d_loc, VectorElemental &elvec, const CurrentFE &fe_u, const CurrentFE &fe_p, int iblock=0) |
![$coef * ( (\nabla u^k):[I\nabla\cdot d - (\nabla d)^T] , q )$](form_40.png) for Newton FSI More... for Newton FSI More... | |
| void | source_press2 (Real coef, const VectorElemental &p_loc, const VectorElemental &d_loc, VectorElemental &elvec, const CurrentFE &fe, int iblock) |
| void | source_press (Real coef, const VectorElemental &uk_loc, MatrixElemental &elmat, const CurrentFE &fe_u, const CurrentFE &fe_p, ID mmDim, int iblock=0) |
![$coef * ( (\nabla u^k):[I\nabla\cdot d - (\nabla d)^T] , q )$](form_40.png) for Newton FSI More... for Newton FSI More... | |
| void | shape_terms ( Real coef, Real mu, const VectorElemental &un_loc, const VectorElemental &uk_loc, const VectorElemental &wk_loc, const VectorElemental &convect_loc, const VectorElemental &pk_loc, MatrixElemental &elmat, const CurrentFE &fe, const CurrentFE &fe_p, ID mmDim, MatrixElemental &, int iblock=0, bool wImplicit=false, Real alpha=0., std::shared_ptr< MatrixElemental > elmat_convect=std::shared_ptr< MatrixElemental >()) |
| Shape terms for the CE system in FSI Newton. More... | |
Mass matrix | |
| void | mass_divw (Real coef, const VectorElemental &w_loc, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, UInt nb) |
| void | mass_divw (const std::vector< Real > &coef, const VectorElemental &w_loc, MatrixElemental &elmat, const CurrentFE &fe, int iblock, int jblock, UInt nb) |
Idem mass_divw | |
| void | mass_gradu (Real coef, const VectorElemental &u0_loc, MatrixElemental &elmat, const CurrentFE &fe) |
Cholesky | |
| void | choldc (KNM< Real > &a, KN< Real > &p) |
| void | cholsl (KNM< Real > &a, KN< Real > &p, KN< Real > &b, KN< Real > &x) |
Operators for H(div) finite elements | |
| void | grad_Hdiv (Real coef, MatrixElemental &elmat, const CurrentFE &dualFE, const CurrentFE &primalFE, int iblock, int jblock) |
| void | div_Hdiv (Real coef, MatrixElemental &elmat, const CurrentFE &dualFE, const CurrentFE &primalFE, int iblock, int jblock) |
| void | TP_VdotN_Hdiv (Real coef, MatrixElemental &elmat, const ReferenceFEHybrid &hybridFE, const ReferenceFEHybrid &dualDotNFE, int iblock, int jblock) |
| void | TP_TP_Hdiv (Real coef, MatrixElemental &elmat, const ReferenceFEHybrid &hybridFE, int iblock, int jblock) |
| void | mass_Hdiv (Real coef, MatrixElemental &elmat, const CurrentFE &dualFE, int iblock, int jblock) |
| void | mass_Hdiv (Matrix const &Invperm, MatrixElemental &elmat, const CurrentFE &dualFE, int iblock, int jblock) |
| void | mass_Hdiv (Real(*InvpermFun)(const Real &, const Real &, const Real &), MatrixElemental &elmat, const CurrentFE &dualFE, int iblock, int jblock) |
| void | source_Hdiv (const Vector &source, VectorElemental &elvec, const CurrentFE &dualFE, int iblock) |
/namespace AssemblyElemental
This namespace is specially designed to contain the elementary operations (corresponding to differential operators) that build the local contributions to be used in the assembly procedures.
| typedef std::function< const Real (const Real&, const Real&, const Real&, const Real&, const ID&) > function_Type |
Use the portable syntax of the boost function.
Definition at line 84 of file AssemblyElemental.hpp.
| void mass | ( | MatrixElemental & | localMass, |
| const CurrentFE & | massCFE, | ||
| const Real & | coefficient, | ||
| const UInt & | fieldDim | ||
| ) |
Elementary mass for constant mass coefficient.
This function assembles the local mass matrix when the mass coefficient is constant.
| localMass | The local matrix to be filled (not cleaned by this function) |
| massCFE | The currentFE structure already updated for the assembly. It requires phi and wDetJacobian to be accessible. |
| coefficient | The mass coefficient |
| fieldDim | The dimension of the FE space (scalar/vectorial) |
Definition at line 46 of file AssemblyElemental.cpp.
| void stiffness | ( | MatrixElemental & | localStiff, |
| const CurrentFE & | stiffCFE, | ||
| const Real & | coefficient, | ||
| const UInt & | fieldDim | ||
| ) |
Elementary stiffness for constant coefficient.
This function assembles the local stiffness matrix when the coefficient is constant.
| localStiff | The local matrix to be filled (not cleaned by this function) |
| stiffCFE | The currentFE structure already updated for the assembly. It requires dphi and wDetJacobian to be accessible. |
| coefficient | The coefficient |
| fieldDim | The dimension of the FE space (scalar/vectorial) |
Definition at line 106 of file AssemblyElemental.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:| void advectionNewton | ( | Real | coef, |
| VectorElemental & | vel, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Assemble the term 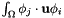 .
.
Definition at line 173 of file AssemblyElemental.cpp.
| void grad | ( | MatrixElemental & | elmat, |
| const CurrentFE & | uCFE, | ||
| const CurrentFE & | pCFE, | ||
| const UInt & | fieldDim | ||
| ) |
Definition at line 204 of file AssemblyElemental.cpp.
| void divergence | ( | MatrixElemental & | elmat, |
| const CurrentFE & | uCFE, | ||
| const CurrentFE & | pCFE, | ||
| const UInt & | fieldDim, | ||
| const Real & | coefficient | ||
| ) |
Definition at line 235 of file AssemblyElemental.cpp.
| void stiffStrain | ( | MatrixElemental & | localStiff, |
| const CurrentFE & | stiffCFE, | ||
| const Real & | coefficient, | ||
| const UInt & | fieldDim | ||
| ) |
Definition at line 267 of file AssemblyElemental.cpp.
| void bodyForces | ( | VectorElemental & | localForce, |
| const CurrentFE & | massRhsCFE, | ||
| const function_Type & | fun, | ||
| const Real & | t, | ||
| const UInt & | fieldDim | ||
| ) |
Definition at line 303 of file AssemblyElemental.cpp.
| void mass | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
coef(t,x,y,z,u)
Definition at line 362 of file AssemblyElemental.cpp.
| void mass | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| UInt | nb | ||
| ) |
Definition at line 405 of file AssemblyElemental.cpp.
| void mass | ( | const std::vector< Real > & | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| UInt | nb | ||
| ) |
Mass term with coefficients given for each quadrature point.
Definition at line 467 of file AssemblyElemental.cpp.
| void stiff_divgrad | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 530 of file AssemblyElemental.cpp.
| void stiff_divgrad_2 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 582 of file AssemblyElemental.cpp.
| void stiff_gradgrad | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 635 of file AssemblyElemental.cpp.
| void stiff_gradgrad_2 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 687 of file AssemblyElemental.cpp.
| void stiff_dergrad_gradbis | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 742 of file AssemblyElemental.cpp.
| void stiff_dergrad_gradbis_Tr | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 800 of file AssemblyElemental.cpp.
| void stiff_dergrad_gradbis_2 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 858 of file AssemblyElemental.cpp.
| void stiff_dergrad_gradbis_Tr_2 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 917 of file AssemblyElemental.cpp.
| void stiff_gradgradTr_gradbis | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 976 of file AssemblyElemental.cpp.
| void stiff_gradgradTr_gradbis_2 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 1038 of file AssemblyElemental.cpp.
| void stiff_gradgradTr_gradbis_3 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 1099 of file AssemblyElemental.cpp.
| void ipstab_grad | ( | const Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| const CurrentFEManifold & | bdfe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
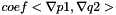
Definition at line 1171 of file AssemblyElemental.cpp.
| void ipstab_grad | ( | const Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| const CurrentFEManifold & | bdfe, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | nb | ||
| ) |
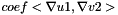
Definition at line 1272 of file AssemblyElemental.cpp.
| void ipstab_bgrad | ( | const Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| const VectorElemental & | beta, | ||
| const CurrentFEManifold & | bdfe, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | nb | ||
| ) |
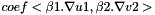
Definition at line 1379 of file AssemblyElemental.cpp.
| void ipstab_div | ( | const Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| const CurrentFEManifold & | bdfe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
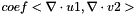
Definition at line 1513 of file AssemblyElemental.cpp.
| void ipstab_bagrad | ( | const Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| const VectorElemental & | beta, | ||
| const CurrentFEManifold & | bdfe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
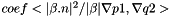
Definition at line 1604 of file AssemblyElemental.cpp.
| void ipstab_bagrad | ( | const Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| const CurrentFE & | fe3, | ||
| const VectorElemental & | beta, | ||
| const CurrentFEManifold & | bdfe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
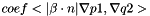 p1 lives in fe1 q2 lives in fe2 beta lives in fe3
p1 lives in fe1 q2 lives in fe2 beta lives in fe3
Definition at line 1727 of file AssemblyElemental.cpp.
| void stiff | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Definition at line 1848 of file AssemblyElemental.cpp.
| void stiff | ( | Real | coef, |
| Real(*)(Real, Real, Real) | fct, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Definition at line 1894 of file AssemblyElemental.cpp.
| void stiff | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | nb | ||
| ) |
Definition at line 1942 of file AssemblyElemental.cpp.
| void stiff | ( | const std::vector< Real > & | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | nb | ||
| ) |
Stiff term with coefficient given for each quadrature node.
Definition at line 2009 of file AssemblyElemental.cpp.
| void stiff_curl | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | |||
| ) |
Definition at line 2077 of file AssemblyElemental.cpp.
| void stiff_div | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
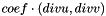
Definition at line 2503 of file AssemblyElemental.cpp.
| void stiff_dergradbis | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
![$ coef \cdot ( [\nabla u^k]^T \nabla u : \nabla v )$](form_18.png)
Definition at line 2539 of file AssemblyElemental.cpp.
| void stiff_dergrad | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
![$ coef \cdot ( [\nabla u]^T \nabla u^k + [\nabla u^k]^T \nabla u : \nabla v )$](form_19.png) for Newton on St-Venant
for Newton on St-Venant
Definition at line 2600 of file AssemblyElemental.cpp.
| void stiff_derdiv | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
![$ coef \cdot ( trace { [\nabla u^k]^T \nabla u }, \nabla\cdot v ) $](form_20.png) for Newton on St-Venant
for Newton on St-Venant
Definition at line 2665 of file AssemblyElemental.cpp.
| void stiff_strain | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
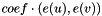
Definition at line 2722 of file AssemblyElemental.cpp.
| void mass_divw | ( | Real | coef, |
| const VectorElemental & | w_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| UInt | nb | ||
| ) |
Weighted Mass matrix with a permeability tensor which is a constant scalar matrix (i.e. 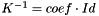 , coef being the inverse of the permeability).
, coef being the inverse of the permeability).
Definition at line 2772 of file AssemblyElemental.cpp.
| void mass_divw | ( | const std::vector< Real > & | coef, |
| const VectorElemental & | w_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| UInt | nb | ||
| ) |
Idem mass_divw , but with coefficient given by quadrature node.
Definition at line 2846 of file AssemblyElemental.cpp.
| void mass_gradu | ( | Real | coef, |
| const VectorElemental & | u0_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 2921 of file AssemblyElemental.cpp.
| void stiff_sd | ( | Real | coef, |
| const VectorElemental & | vec_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| const CurrentFE & | fe2, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | nb | ||
| ) |
StreamLine Diffusion.
Definition at line 2980 of file AssemblyElemental.cpp.
| void grad | ( | const int | icoor, |
| Real | coef, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe_u, | ||
| const CurrentFE & | fe_p, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Definition at line 3085 of file AssemblyElemental.cpp.
| void div | ( | const int | icoor, |
| Real | coef, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe_u, | ||
| const CurrentFE & | fe_p, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Definition at line 3114 of file AssemblyElemental.cpp.
| void grad_div | ( | Real | coef_grad, |
| Real | coef_div, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe_u, | ||
| const CurrentFE & | fe_p, | ||
| int | block_pres | ||
| ) |
Definition at line 3139 of file AssemblyElemental.cpp.
| void stab_stokes | ( | Real | visc, |
| Real | coef_stab, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | block_pres | ||
| ) |
Definition at line 3168 of file AssemblyElemental.cpp.
| void advection | ( | Real | coef, |
| VectorElemental & | vel, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | nb | ||
| ) |
Definition at line 3194 of file AssemblyElemental.cpp.
| void grad | ( | const int | icoor, |
| const VectorElemental & | vec_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Convective term with a local vector coefficient (useful for Navier-Stokes problem)
Definition at line 3250 of file AssemblyElemental.cpp.
| void grad_ss | ( | const int | icoor, |
| const VectorElemental & | vec_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Convective term with a local vector coefficient for Navier-Stokes problem in Skew-Symmetric form.
Definition at line 3293 of file AssemblyElemental.cpp.
| void grad | ( | const int | icoor, |
| const VectorElemental & | vec_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe1, | ||
| const CurrentFE & | fe2, | ||
| const CurrentFE & | fe3, | ||
| int | iblock, | ||
| int | jblock | ||
| ) |
Convective term with a local vector coefficient (useful for Navier-Stokes problem+adv-diff)
Definition at line 3340 of file AssemblyElemental.cpp.
| void grad | ( | const int & | icoor, |
| const std::vector< Real > & | localVector, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | currentFE1, | ||
| const CurrentFE & | currentFE2, | ||
| const int & | iblock = 0, |
||
| const int & | jblock = 0 |
||
| ) |
Conective term with a local vector given by quadrature node.
To use this function, we must ensure that the velocity is stored in a good way in the std::vector: If there are nQ quadrature nodes, the i-th component (starting from 0) of the velocity in the iq-th quadrature node (also starting from 0) has to be stored in the ( i*nQ + iq)-th element of the std::vector.
Definition at line 3388 of file AssemblyElemental.cpp.
| void source | ( | Real | constant, |
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe, | ||
| int | iblock | ||
| ) |
Definition at line 3483 of file AssemblyElemental.cpp.
| void source | ( | Real | coef, |
| VectorElemental & | f, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe, | ||
| int | fblock, | ||
| int | eblock | ||
| ) |
Definition at line 3499 of file AssemblyElemental.cpp.
| void source_mass | ( | const std::vector< Real > & | constant, |
| VectorElemental & | elvec, | ||
| const CurrentFE & | currentFe, | ||
| const int & | iblock | ||
| ) |
Assembly for the source term 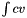 where
where 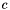 is a given by the values in the quadrature nodes.
is a given by the values in the quadrature nodes.
This function add in the elementary vector the term 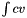 . The function
. The function 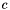 is given by its values in the quadrature nodes.
is given by its values in the quadrature nodes.
| constant | Values of the function in the quadrature nodes |
| elvec | The local vector where to add the values |
| currentFe | The currentFE associated to the cell where to assemble |
| iblock | The component of v that is concerned |
Definition at line 3528 of file AssemblyElemental.cpp.
| void source_stiff | ( | const std::vector< Real > & | constant, |
| VectorElemental & | elvec, | ||
| const CurrentFE & | currentFe, | ||
| const int & | iblock | ||
| ) |
Assembly for the source term 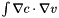 where
where 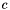 is a given by the values in the quadrature nodes.
is a given by the values in the quadrature nodes.
The function 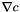 is given by its values in the quadrature nodes, coordinate after coordinate (first, the values for the first componant of the gradient in all the quadrature nodes, then second component,...).
is given by its values in the quadrature nodes, coordinate after coordinate (first, the values for the first componant of the gradient in all the quadrature nodes, then second component,...).
| constant | Values of the gradient in the quadrature nodes |
| elvec | The local vector where to add the values |
| currentFe | The currentFE associated to the cell where to assemble |
| iblock | The component of v that is concerned |
Definition at line 3542 of file AssemblyElemental.cpp.
| void source_divuq | ( | Real | alpha, |
| VectorElemental & | uLoc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe_u, | ||
| const CurrentFE & | fe_p, | ||
| int | iblock | ||
| ) |
Definition at line 3562 of file AssemblyElemental.cpp.
| void source_gradpv | ( | Real | alpha, |
| VectorElemental & | pLoc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe_p, | ||
| const CurrentFE & | fe_u, | ||
| int | iblock | ||
| ) |
Definition at line 3583 of file AssemblyElemental.cpp.
| void source_fhn | ( | Real | coef_f, |
| Real | coef_a, | ||
| VectorElemental & | u, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe, | ||
| int | fblock, | ||
| int | eblock | ||
| ) |
Definition at line 3604 of file AssemblyElemental.cpp.
| void source_advection | ( | const Real & | coefficient, |
| const VectorElemental & | beta_loc, | ||
| const VectorElemental & | uk_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe | ||
| ) |
| void source_mass1 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| const VectorElemental & | wk_loc, | ||
| const VectorElemental & | convect_loc, | ||
| const VectorElemental & | d_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe | ||
| ) |
| void source_mass2 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| const VectorElemental & | dw_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe | ||
| ) |
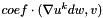 for Newton FSI
for Newton FSI
Definition at line 3871 of file AssemblyElemental.cpp.
| void source_mass3 | ( | Real | coef, |
| const VectorElemental & | un_loc, | ||
| const VectorElemental & | uk_loc, | ||
| const VectorElemental & | d_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe | ||
| ) |
Definition at line 3956 of file AssemblyElemental.cpp.
| void source_stress | ( | Real | coef, |
| Real | mu, | ||
| const VectorElemental & | uk_loc, | ||
| const VectorElemental & | pk_loc, | ||
| const VectorElemental & | d_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe_u, | ||
| const CurrentFE & | fe_p | ||
| ) |
![$coef \cdot ( [-p^k I + 2\mu e(u^k)] [I\nabla\cdot d - (\nabla d)^T] , \nabla v )$](form_37.png) for Newton FSI
for Newton FSI
Definition at line 4063 of file AssemblyElemental.cpp.
| void source_stress2 | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| const VectorElemental & | d_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe_u | ||
| ) |
![$+ \mu ( \nabla u^k \nabla d + [\nabla d]^T[\nabla u^k]^T : \nabla v )$](form_38.png)
Definition at line 4194 of file AssemblyElemental.cpp.
| void source_press | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| const VectorElemental & | d_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe_u, | ||
| const CurrentFE & | fe_p, | ||
| int | iblock | ||
| ) |
![$coef * ( (\nabla u^k):[I\nabla\cdot d - (\nabla d)^T] , q )$](form_40.png) for Newton FSI
for Newton FSI
Definition at line 4290 of file AssemblyElemental.cpp.
| void source_press2 | ( | Real | coef, |
| const VectorElemental & | p_loc, | ||
| const VectorElemental & | d_loc, | ||
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe, | ||
| int | iblock | ||
| ) |
Definition at line 4371 of file AssemblyElemental.cpp.
Cholesky decomposition and solution for a KNM matrix.
Definition at line 4470 of file AssemblyElemental.cpp.
Definition at line 4497 of file AssemblyElemental.cpp.
| void source_press | ( | Real | coef, |
| const VectorElemental & | uk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe_u, | ||
| const CurrentFE & | fe_p, | ||
| ID | mmDim, | ||
| int | iblock | ||
| ) |
![$coef * ( (\nabla u^k):[I\nabla\cdot d - (\nabla d)^T] , q )$](form_40.png) for Newton FSI
for Newton FSI
fe_u.phi( i, ig )
d_loc.vec() [ i + jcoor * fe_u.nbFEDof() ];
Definition at line 4524 of file AssemblyElemental.cpp.
| void shape_terms | ( | Real | coef, |
| Real | mu, | ||
| const VectorElemental & | un_loc, | ||
| const VectorElemental & | uk_loc, | ||
| const VectorElemental & | wk_loc, | ||
| const VectorElemental & | convect_loc, | ||
| const VectorElemental & | pk_loc, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| const CurrentFE & | fe_p, | ||
| ID | mmDim, | ||
| MatrixElemental & | , | ||
| int | iblock = 0, |
||
| bool | wImplicit = false, |
||
| Real | alpha = 0., |
||
| std::shared_ptr< MatrixElemental > | elmat_convect = std::shared_ptr< MatrixElemental >() |
||
| ) |
Shape terms for the CE system in FSI Newton.
It is the sum of the terms source_mass1 ,source_stress difference between this method and the previous ones is that here the shape terms are assembled in a matrix, instead of a vector. This implies some extra loop and the explicit construction of the tensor and source_stress2 the.![$[I\nabla\cdot d - (\nabla d)^T]$](form_39.png) instead of it's multiplication times a vector. However the computation of these terms need to be done once per Newton iterations, instead of once per Jacobian-vector multiplication.
instead of it's multiplication times a vector. However the computation of these terms need to be done once per Newton iterations, instead of once per Jacobian-vector multiplication.
Note that the term source_mass2 considered if the fluid domain velocity w is trated explicitly. This method is currently tested only for the P1-P1 stabilized space discretization. is not
d_loc.vec() [ i + jcoor * fe.nbFEDof() ]
d_loc.vec() [ i + jcoor * fe.nbFEDof() ]
a part of source_stress
building the tensor ![$\eta = [I\nabla\cdot d - (\nabla d)^T]$](form_14.png)
source_mass1
source_stress
source_stress2
alpha
building the tensor ![$\eta = [I\nabla\cdot d - (\nabla d)^T]$](form_14.png)
-2*{jcoor, kcoor} {icoor} + {jcoor, icoor}{kcoor}
Definition at line 4714 of file AssemblyElemental.cpp.
| void grad_Hdiv | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | dualFE, | ||
| const CurrentFE & | primalFE, | ||
| int | iblock = 0, |
||
| int | jblock = 0 |
||
| ) |
Compute the gradient of an element in 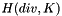 space, i.e. the opposite of the transpose divergence matrix, with
space, i.e. the opposite of the transpose divergence matrix, with 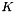 the current element. In formula
the current element. In formula
![\[ \mathrm{coef} < \nabla q, w > \equiv - \mathrm{coef} < q, \nabla \cdot w > \,, \]](form_44.png)
for 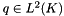 ,
, 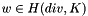 and
and 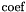 a real scalar.
a real scalar.
| coef | Constant real coefficient. |
| elmat | Mixed element matrix. |
| dualFE | Current dual finite element in 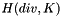 . . |
| primalFE | Current primal finite element in 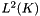 . . |
| iblock | Subarray index where to store the integral just computed. |
| jblock | Subarray index where to store the integral just computed. |
Definition at line 5079 of file AssemblyElemental.cpp.
| void div_Hdiv | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | dualFE, | ||
| const CurrentFE & | primalFE, | ||
| int | iblock = 0, |
||
| int | jblock = 0 |
||
| ) |
Compute the divergence of an element in 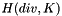 , with
, with 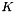 the current element. In formula
the current element. In formula
![\[ \mathrm{coef} < q, \nabla \cdot w > \,, \]](form_51.png)
for 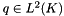 ,
, 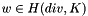 and
and 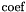 a real scalar.
a real scalar.
| coef | Constant real coefficient. |
| elmat | Mixed element matrix. |
| dualFE | Current dual finite element in 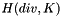 . . |
| primalFE | Current primal finite element in 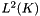 . . |
| iblock | Subarray index where to store the integral just computed. |
| jblock | Subarray index where to store the integral just computed. |
Definition at line 5105 of file AssemblyElemental.cpp.
| void TP_VdotN_Hdiv | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const ReferenceFEHybrid & | hybridFE, | ||
| const ReferenceFEHybrid & | dualDotNFE, | ||
| int | iblock = 0, |
||
| int | jblock = 0 |
||
| ) |
Compute the product between an hybrid variable and a dual variable dot product outward unit normal, in the current element 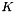 . In formula
. In formula
![\[ \mathrm{coef} < \lambda, v \cdot n >\,, \]](form_52.png)
for 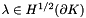 ,
, 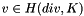 ,
, 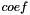 a real scalar and
a real scalar and 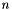 the normal unit vector oriented outward of the current element
the normal unit vector oriented outward of the current element 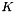 .
.
The 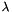 are the Lagrange multiplier basis functions that enforce continuity of the normal component of the vectorial functions across two neighbouring elements. They can be interprated as trace of primal variable.
are the Lagrange multiplier basis functions that enforce continuity of the normal component of the vectorial functions across two neighbouring elements. They can be interprated as trace of primal variable.
See Hybridization for Mixed Hybrid Finite Element Method.
Thanks to the Piola transform, the computation is performed on the boundary of the reference element. But in general, the boundary of a 3D reference element is not a 2D reference element.
Example: REFERENCE TETRA -> 3 REFERENCE TRIA + 1 EQUILATERAL TRIANGLE... REFERENCE PRISM -> 2 TRIA + 3 QUAD...? REFERENCE HEXA -> 6 REFERENCE QUAD.
| coef | Constant real coefficient. |
| elmat | Mixed element matrix. |
| hybridFE | Reference hybrid finite element. |
| dualDotNFE | Reference dual dot product outward unit normal finite element. |
| iblock | Subarray index where to store the integral just computed. |
| jblock | Subarray index where to store the integral just computed. |
Definition at line 5131 of file AssemblyElemental.cpp.
| void TP_TP_Hdiv | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const ReferenceFEHybrid & | hybridFE, | ||
| int | iblock = 0, |
||
| int | jblock = 0 |
||
| ) |
Compute the mass matrix for the hybrid variable, in the current element 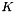 . In formula
. In formula
![\[ \mathrm{coef} < \lambda, \mu > \,, \]](form_57.png)
for 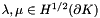 and
and 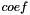 a real scalar.
a real scalar.
The 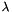 and
and 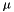 are the Lagrange multiplier basis functions that enforce continuity of the normal component of the vectorial functions across two neighbouring elements. They can be interprated as trace of primal variable.
are the Lagrange multiplier basis functions that enforce continuity of the normal component of the vectorial functions across two neighbouring elements. They can be interprated as trace of primal variable.
See Hybridization for Mixed Hybrid Finite Element Method.
Thanks to the Piola transform, the computation is performed on the boundary of the reference element. But in general, the boundary of a 3D Reference element is not a 2D reference element.
Example: REFERENCE TETRA -> 3 REFERENCE TRIA + 1 EQUILATERAL TRIANGLE... REFERENCE PRISM -> 2 TRIA + 3 QUAD...? REFERENCE HEXA -> 6 REFERENCE QUAD.
| coef | Constant real coefficient. |
| elmat | Mixed element matrix. |
| hybridFE | Reference hybrid finite element. |
| iblock | Subarray index where to store the integral just computed. |
| jblock | Subarray index where to store the integral just computed. |
Definition at line 5171 of file AssemblyElemental.cpp.
| void mass_Hdiv | ( | Real | coef, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | dualFE, | ||
| int | iblock = 0, |
||
| int | jblock = 0 |
||
| ) |
Compute the mass matrix in 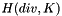 with constant real permeability, with
with constant real permeability, with 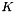 the current element. In formula
the current element. In formula
![\[ \mathrm{coef} < u, w > \,, \]](form_60.png)
for 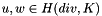 and
and 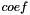 a real scalar.
a real scalar.
Weighted Mass matrix with a permeability tensor which is a constant scalar matrix, i.e. 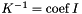 ,
, 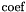 being the inverse of the permeability.
being the inverse of the permeability.
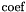 that is used, and not its inverse.
that is used, and not its inverse. | coef | Constant real coefficient. |
| elmat | Mixed element matrix. |
| dualFE | Current dual finite element in 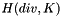 . . |
| iblock | Subarray index where to store the integral just computed. |
| jblock | Subarray index where to store the integral just computed. |
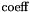 is the inverse of the permeability coefficient.
is the inverse of the permeability coefficient. Definition at line 5208 of file AssemblyElemental.cpp.
| void mass_Hdiv | ( | Matrix const & | Invperm, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | dualFE, | ||
| int | iblock = 0, |
||
| int | jblock = 0 |
||
| ) |
Compute the mass matrix in 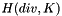 with constant matrix permeability, with
with constant matrix permeability, with 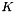 the current element. In formula
the current element. In formula
![\[ < \mathrm{Invperm}\, u, w > \,, \]](form_64.png)
for 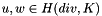 and
and 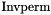 a real constant matrix.
a real constant matrix.
Weighted mass matrix in 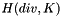 with permeability matrix which is a constant per element symmetric positive definite matrix, non diagonal a priori, and already inverted, with Lapack LU or Choleski for instance.
with permeability matrix which is a constant per element symmetric positive definite matrix, non diagonal a priori, and already inverted, with Lapack LU or Choleski for instance.
| Invperm | Constant coefficient tensor, constant means constant over the current element. |
| elmat | Mixed element matrix. |
| dualFE | Current dual finite element in 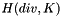 . . |
| iblock | Subarray index where to store the integral just computed. |
| jblock | Subarray index where to store the integral just computed. |
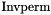 is the inverse of the permeability matrix.
is the inverse of the permeability matrix. Definition at line 5237 of file AssemblyElemental.cpp.
| void mass_Hdiv | ( | Real(*)(const Real &, const Real &, const Real &) | InvpermFun, |
| MatrixElemental & | elmat, | ||
| const CurrentFE & | dualFE, | ||
| int | iblock = 0, |
||
| int | jblock = 0 |
||
| ) |
Compute the mass matrix in 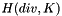 with real function permeability, with
with real function permeability, with 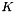 the current element. In formula
the current element. In formula
![\[ < \mathrm{InvpermFun}\, u, w > \,, \]](form_66.png)
for 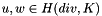 and
and 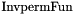 a real function.
a real function.
Weighted mass matrix with a permeability that is a scalar function. The inverse function of the permeability should be provided. We note again that it is the inverse of the permeability that is provided directly 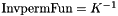 .
.
| InvpermFun | Scalar function inverse of the permeability. |
| elmat | Mixed element matrix. |
| dualFE | Current dual finite element in 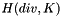 . . |
| iblock | Subarray index where to store the integral just computed. |
| jblock | Subarray index where to store the integral just computed. |
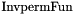 is the inverse of the permeability function.
is the inverse of the permeability function. Definition at line 5277 of file AssemblyElemental.cpp.
| void source_Hdiv | ( | const Vector & | source, |
| VectorElemental & | elvec, | ||
| const CurrentFE & | dualFE, | ||
| int | iblock = 0 |
||
| ) |
Compute the source vector in 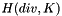 with constant vector permeability, with
with constant vector permeability, with 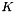 the current element. In formula
the current element. In formula
![\[ < g, w > \,, \]](form_69.png)
for 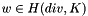 and
and 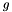 a constant vector.
a constant vector.
| source | constant vector as the source. |
| elvect | element vector. |
| dualFE | Current dual finite element in 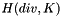 . . |
| iblock | Subarray index where to store the integral just computed. |
Definition at line 5315 of file AssemblyElemental.cpp.
| void LifeV::AssemblyElemental::weightedMass | ( | MatrixElemental & | localMass, |
| const CurrentFE & | massCFE, | ||
| const Real & | coefficient, | ||
| const localVector & | localValues, | ||
| const UInt & | fieldDim | ||
| ) |
Elementary weighted mass for constant mass coefficient.
This function assembles the local mass matrix when the mass coefficient is constant.
| localMass | The local matrix to be filled (not cleaned by this function) |
| massCFE | The currentFE structure already updated for the assembly. It requires phi and wDetJacobian to be accessible. |
| coefficient | The mass coefficient |
| fieldDim | The dimension of the FE space (scalar/vectorial) |
Definition at line 113 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::interpolate | ( | localVector & | localValues, |
| const CurrentFE & | interpCFE, | ||
| const UInt & | spaceDim, | ||
| const DOF & | betaDof, | ||
| const UInt & | elementID, | ||
| const globalVector & | beta | ||
| ) |
Interpolation procedure.
Definition at line 185 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::interpolateGradient | ( | localVector & | localGradient, |
| const CurrentFE & | interpCFE, | ||
| const UInt & | spaceDim, | ||
| const DOF & | betaDof, | ||
| const UInt & | elementID, | ||
| const globalVector & | beta | ||
| ) |
Interpolation of the gradient.
Definition at line 216 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::interpolateDivergence | ( | localVector & | localDivergence, |
| const CurrentFE & | interpCFE, | ||
| const DOF & | betaDof, | ||
| const UInt & | elementID, | ||
| const globalVector & | beta | ||
| ) |
Interpolation of the divergence.
Definition at line 249 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::massDivW | ( | MatrixElemental & | localMass, |
| const CurrentFE & | massCFE, | ||
| const Real & | coefficient, | ||
| const localVector & | localValues, | ||
| const UInt & | fieldDim | ||
| ) |
Definition at line 277 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::advection | ( | MatrixElemental & | localAdv, |
| const CurrentFE & | advCFE, | ||
| const Real & | coefficient, | ||
| const localVector & | localValues, | ||
| const UInt & | fieldDim | ||
| ) |
Elementary advection u v.
Definition at line 327 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::symmetrizedAdvection | ( | MatrixElemental & | localAdv, |
| const CurrentFE & | advCFE, | ||
| const Real & | coefficient, | ||
| const localTensor & | localGradient, | ||
| const UInt & | fieldDim | ||
| ) |
Elementary advection, term u v.
Definition at line 385 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::advection | ( | Real | coef, |
| const UsrFct & | beta, | ||
| MatrixElemental & | elmat, | ||
| const CurrentFE & | fe, | ||
| int | iblock, | ||
| int | jblock, | ||
| int | nb, | ||
| Real | t = 0. |
||
| ) |
Definition at line 555 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::source | ( | Real | constant, |
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe, | ||
| Real | t, | ||
| int | iblock | ||
| ) |
| void LifeV::AssemblyElemental::source | ( | const UsrFct & | fct, |
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe, | ||
| int | iblock = 0 |
||
| ) |
source 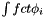
Definition at line 727 of file AssemblyElemental.hpp.
| void LifeV::AssemblyElemental::source | ( | const UsrFct & | fct, |
| VectorElemental & | elvec, | ||
| const CurrentFE & | fe, | ||
| Real | t, | ||
| int | iblock = 0 |
||
| ) |
source 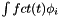
Definition at line 749 of file AssemblyElemental.hpp.