 |
LifeV
|
 |
LifeV
|
StabilizationIP Class. More...
#include <StabilizationIP.hpp>
 Collaboration diagram for StabilizationIP< MeshType, DofType >:
Collaboration diagram for StabilizationIP< MeshType, DofType >:Public Types | |
| typedef std::shared_ptr< MeshType > | mesh_type |
| typedef MeshType | mesh_Type |
| typedef DofType | dof_Type |
| typedef std::shared_ptr< mesh_Type > | meshPtr_Type |
| typedef std::shared_ptr< dof_Type > | dofPtr_Type |
Constructor and Destructor | |
| StabilizationIP () | |
| Default Constructor. More... | |
| virtual | ~StabilizationIP () |
Methods | |
| template<typename MatrixType , typename VectorType > | |
| void | apply (MatrixType &matrix, const VectorType &state, bool verbose=true) |
| compute IP stabilization terms and add them into matrix More... | |
| void | showMe (std::ostream &output=std::cout) const |
| Display class informations. More... | |
Set Methods | |
| void | setGammaBeta (const Real &gammaBeta) |
Set the stabilization parameter 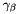 for for ![$\Sigma_{f\in\mathcal{F}}\int_{f} [\beta \cdot \nabla \mathbf{u}] [\beta \cdot \nabla \mathbf{v}]$](form_464.png) . More... . More... | |
| void | setGammaDiv (const Real &gammaDiv) |
Set the stabilization parameter 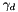 for for ![$\Sigma_{f\in\mathcal{F}}\int_{f} [div \mathbf{u}] [div \mathbf{v}]$](form_466.png) . More... . More... | |
| void | setGammaPress (const Real &gammaPress) |
Set the stabilization parameter 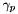 for for ![$\Sigma_{f\in\mathcal{F}}\int_{f} [\nabla p] \cdot [\nabla q]$](form_468.png) . More... . More... | |
| void | setViscosity (const Real &viscosity) |
Set the fluid viscosity 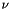 . More... . More... | |
| void | setMesh (const meshPtr_Type mesh) |
| Set the mesh file. More... | |
| void | setDiscretization (const dofPtr_Type &dof, const ReferenceFE &refFE, CurrentFEManifold &feBd, const QuadratureRule &quadRule) |
| Set Discretization. More... | |
| template<typename MapType > | |
| void | setFeSpaceVelocity (FESpace< mesh_Type, MapType > &feSpaceVelocity) |
| Set the fespace. More... | |
Private Types | |
| typedef ID(* | FTOP) (ID const &localFacet, ID const &point) |
| facetToPoint(i,j) = localId of jth point on ith local facet More... | |
Private Constructor | |
| StabilizationIP (const StabilizationIP< mesh_Type, dof_Type > &original) | |
| Copy Constructor. More... | |
Private Attributes | |
| meshPtr_Type | M_mesh |
| Pointer to the mesh object. More... | |
| dofPtr_Type | M_dof |
| reference to the DofType data structure More... | |
| std::shared_ptr< CurrentFE > | M_feOnSide1 |
| current Fe on side 1 of the current facet More... | |
| std::shared_ptr< CurrentFE > | M_feOnSide2 |
| current Fe on side 2 of the current facet More... | |
| CurrentFEManifold * | M_feBd |
| current boundary FE More... | |
| Real | M_gammaBeta |
Stabilization parameter 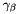 for for ![$\int_{facet} [\beta \cdot \nabla \mathbf{u}] [\beta \cdot \nabla \mathbf{v}]$](form_470.png) . More... . More... | |
| Real | M_gammaDiv |
Stabilization parameter 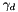 for for ![$\int_{facet} [div \mathbf{u}] [div \mathbf{v}]$](form_471.png) . More... . More... | |
| Real | M_gammaPress |
Stabilization parameter 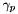 for for ![$\int_{facet} [\nabla p] \cdot [\nabla q]$](form_472.png) . More... . More... | |
| Real | M_viscosity |
Fluid viscosity 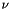 . More... . More... | |
| FTOP | M_facetToPoint |
| facetToPoint(i,j) = localId of jth point on ith local facet More... | |
StabilizationIP Class.
Interior Penality Stabilization
Implementation of I.P. stabilization for inf-sup incompatible finite elements for the Navier-Stokes equations.
This function adds the following stabilization terms to the Navier-Stokes monolithic matrix:
![$\Sigma_{f\in\mathcal{F}}\int_{f} c_\beta [\beta \cdot \nabla \mathbf{u}] [\beta \cdot \nabla \mathbf{v}] + \Sigma_{f\in\mathcal{F}}\int_{f} c_d [div \mathbf{u}] [div \mathbf{v}]$](form_450.png)
![$\Sigma_{f\in\mathcal{F}}\int_{f} c_p [\nabla p] \cdot [\nabla q]$](form_451.png)
where
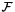 is the set of all the internal facets in the mesh;
is the set of all the internal facets in the mesh; ![$[\cdot]$](form_453.png) is the jump operator:
is the jump operator: ![$[x] = x^+ - x^-$](form_454.png) .
. and the parameter 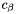 ,
, 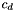 ,
, 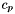 , are defined as follows:
, are defined as follows:
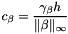 , being
, being 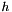 the facet measure;
the facet measure; 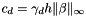 ;
; 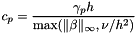 .
. Both high Pechlet numbers and inf-sup incompatible FEM are stabilized.
Definition at line 91 of file StabilizationIP.hpp.
Definition at line 97 of file StabilizationIP.hpp.
Definition at line 98 of file StabilizationIP.hpp.
| typedef DofType dof_Type |
Definition at line 99 of file StabilizationIP.hpp.
| typedef std::shared_ptr<mesh_Type> meshPtr_Type |
Definition at line 100 of file StabilizationIP.hpp.
| typedef std::shared_ptr<dof_Type> dofPtr_Type |
Definition at line 101 of file StabilizationIP.hpp.
facetToPoint(i,j) = localId of jth point on ith local facet
Definition at line 189 of file StabilizationIP.hpp.
| StabilizationIP | ( | ) |
Default Constructor.
Definition at line 229 of file StabilizationIP.hpp.
|
inlinevirtual |
Definition at line 110 of file StabilizationIP.hpp.
|
private |
Copy Constructor.
| void apply | ( | MatrixType & | matrix, |
| const VectorType & | state, | ||
| bool | verbose = true |
||
| ) |
compute IP stabilization terms and add them into matrix
This function adds the following stabilization terms to the Navier-Stokes monolithic matrix:
![$\Sigma_{f\in\mathcal{F}}\int_{f} c_\beta [\beta \cdot \nabla \mathbf{u}] [\beta \cdot \nabla \mathbf{v}] + \Sigma_{f\in\mathcal{F}}\int_{f} c_d [div \mathbf{u}] [div \mathbf{v}]$](form_450.png)
![$\Sigma_{f\in\mathcal{F}}\int_{f} c_p [\nabla p] \cdot [\nabla q]$](form_451.png)
where
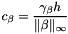 , being
, being 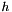 the facet measure;
the facet measure; 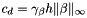 ;
; 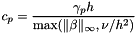 .
. Both high Pechlet numbers and inf-sup incompatible FEM are stabilized.
PREREQUISITE: The velocity and the pressure field should belong to the same finite element space
Parameters are the followings:
| dt | Real timestep (INPUT) |
| matrix | MatrixType where the stabilization terms are added into. (OUTPUT) |
| state | VectorType velocity field for the linearization of the stabilization (INPUT) |
| verbose | bool whenever of not to print on screen |
Definition at line 242 of file StabilizationIP.hpp.
| void showMe | ( | std::ostream & | output = std::cout | ) | const |
Display class informations.
Write information relative to the class on output
| output | ostream ostream were to write (Default cout) |
Definition at line 572 of file StabilizationIP.hpp.
|
inline |
Set the stabilization parameter 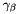 for
for ![$\Sigma_{f\in\mathcal{F}}\int_{f} [\beta \cdot \nabla \mathbf{u}] [\beta \cdot \nabla \mathbf{v}]$](form_464.png) .
.
Definition at line 154 of file StabilizationIP.hpp.
|
inline |
Set the stabilization parameter 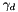 for
for ![$\Sigma_{f\in\mathcal{F}}\int_{f} [div \mathbf{u}] [div \mathbf{v}]$](form_466.png) .
.
Definition at line 159 of file StabilizationIP.hpp.
|
inline |
Set the stabilization parameter 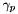 for
for ![$\Sigma_{f\in\mathcal{F}}\int_{f} [\nabla p] \cdot [\nabla q]$](form_468.png) .
.
Definition at line 164 of file StabilizationIP.hpp.
|
inline |
Set the fluid viscosity 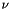 .
.
Definition at line 169 of file StabilizationIP.hpp.
|
inline |
Set the mesh file.
Definition at line 174 of file StabilizationIP.hpp.
| void setDiscretization | ( | const dofPtr_Type & | dof, |
| const ReferenceFE & | refFE, | ||
| CurrentFEManifold & | feBd, | ||
| const QuadratureRule & | quadRule | ||
| ) |
Set Discretization.
Definition at line 587 of file StabilizationIP.hpp.
Set the fespace.
Definition at line 599 of file StabilizationIP.hpp.
|
private |
Pointer to the mesh object.
Definition at line 201 of file StabilizationIP.hpp.
|
private |
reference to the DofType data structure
Definition at line 203 of file StabilizationIP.hpp.
|
private |
current Fe on side 1 of the current facet
Definition at line 205 of file StabilizationIP.hpp.
|
private |
current Fe on side 2 of the current facet
Definition at line 207 of file StabilizationIP.hpp.
|
private |
current boundary FE
Definition at line 209 of file StabilizationIP.hpp.
|
private |
Stabilization parameter 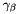 for
for ![$\int_{facet} [\beta \cdot \nabla \mathbf{u}] [\beta \cdot \nabla \mathbf{v}]$](form_470.png) .
.
Definition at line 211 of file StabilizationIP.hpp.
|
private |
Stabilization parameter 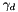 for
for ![$\int_{facet} [div \mathbf{u}] [div \mathbf{v}]$](form_471.png) .
.
Definition at line 213 of file StabilizationIP.hpp.
|
private |
Stabilization parameter 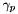 for
for ![$\int_{facet} [\nabla p] \cdot [\nabla q]$](form_472.png) .
.
Definition at line 215 of file StabilizationIP.hpp.
|
private |
Fluid viscosity 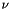 .
.
Definition at line 217 of file StabilizationIP.hpp.
|
private |
facetToPoint(i,j) = localId of jth point on ith local facet
Definition at line 219 of file StabilizationIP.hpp.