 |
LifeV
|
 |
LifeV
|
TimeAdvanceBDFVariableStep - Backward differencing formula time discretization with non-uniform time step. More...
#include <TimeAdvanceBDFVariableStep.hpp>
 Collaboration diagram for TimeAdvanceBDFVariableStep< FEVectorType >:
Collaboration diagram for TimeAdvanceBDFVariableStep< FEVectorType >:Private Attributes | |
| UInt | M_order |
| Order of the BDF derivative/extrapolation: the time-derivative coefficients vector has size n+1, the extrapolation vector has size n. More... | |
| container_Type | M_alpha |
Coefficients 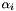 of the time bdf discretization. More... of the time bdf discretization. More... | |
| container_Type | M_beta |
Coefficients 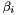 of the extrapolation. More... of the extrapolation. More... | |
| container_Type | M_timeStep |
container_Type 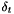 of time intervals More... of time intervals More... | |
| container_Type | M_timeStepBack |
| feVectorPtrContainer_Type | M_unknowns |
| Last n state vectors. More... | |
| feVectorPtrContainer_Type | M_unknownsBack |
Public Types | |
| typedef ScalarVector | container_Type |
| typedef FEVectorType | feVector_Type |
| typedef std::shared_ptr< feVector_Type > | feVectorPtr_Type |
| typedef std::vector< feVectorPtr_Type > | feVectorPtrContainer_Type |
Constructor & Destructor | |
| TimeAdvanceBDFVariableStep () | |
| Empty constructor. More... | |
| ~TimeAdvanceBDFVariableStep () | |
| Destructor. More... | |
Methods | |
| void | setup (const UInt order) |
| Setup the TimeAdvanceBDFVariableStep with order n. More... | |
| void | setInitialCondition (feVector_Type u0, Real const timeStep, bool startup=0) |
| Initialize all the entries of the unknown vector to be derived with the vector u0 (duplicated if startup=0) More... | |
| void | setInitialCondition (std::vector< feVector_Type > u0s, Real const timeStep) |
| Initialize all the entries of the unknown vector to be derived with a set of vectors u0s. More... | |
| template<typename FunctionType , typename FESpaceType > | |
| void | setInitialCondition (const FunctionType &u0Function, feVector_Type &u0Vector, FESpaceType &feSpace, Real t0, Real timeStep) |
| Initialize all the entries of the unknonwn vectors with a given function. More... | |
| feVector_Type | rhsContribution () const |
Returns the right hand side 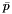 of the time derivative formula divided by dt. More... of the time derivative formula divided by dt. More... | |
| feVector_Type | rhsContributionTimeStep (Real timeStep=1) const |
Returns the right hand side 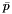 of the time derivative formula divided by timeStep (backward compatibility version, will be discontinued) More... of the time derivative formula divided by timeStep (backward compatibility version, will be discontinued) More... | |
| feVector_Type | extrapolateSolution () const |
| Compute the polynomial extrapolation approximation of order n-1 of u^{n+1} defined by the n stored state vectors. More... | |
| void | shiftRight (feVector_Type const &uCurrent) |
| Update the vectors of the previous time steps by shifting on the right the old values. More... | |
| void | shiftRight (feVector_Type const &uCurrent, Real timeStepNew) |
| Update the vectors of the previous time steps by shifting on the right the old values. More... | |
| void | storeSolution () |
| Save the current vector M_unknowns and the current vector M_timeStep. More... | |
| void | restoreSolution () |
| Restore the vector M_unknowns and the vector M_timeStep with the ones saved with store_unk() More... | |
| void | restoreSolution (Real timeStep) |
| It is equivalent to do : storeSolution() + setTimeStep() More... | |
| void | showMe () const |
| Show informations about the BDF. More... | |
Set Methods | |
| void | setTimeStep (Real timeStep) |
| Replace the current time-step with timeStep and computes the coefficients a_i and beta_i as functions of M_timeStep. More... | |
Get Methods | |
| const Real & | coefficientDerivative (UInt i) const |
| Return the i-th coefficient of the time derivative alpha_i. More... | |
| Real | coefficientDerivativeOverTimeStep (UInt i) const |
| Return the i-th coefficient of the time derivative alpha_i divided by dt. More... | |
| const Real & | coefficientExtrapolation (UInt i) const |
| Return the i-th coefficient of the time extrapolation beta_i. More... | |
| const container_Type & | timeStepVector () const |
| Return the vector of the time steps, ordered starting from the most recent one. More... | |
| const feVectorPtrContainer_Type & | stateVector () const |
| Return a vector with the last n state vectors. More... | |
| const feVectorPtrContainer_Type & | stateVectorBack () const |
| void | computeCoefficient () |
| Private methods. More... | |
TimeAdvanceBDFVariableStep - Backward differencing formula time discretization with non-uniform time step.
A differential equation of the form
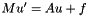
is discretized in time as
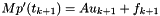
where p denotes the polynomial of order n in t that interpolates 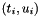 for i = k-n+1,...,k+1.
for i = k-n+1,...,k+1.
The approximative time derivative 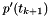 is a linear combination of state vectors
is a linear combination of state vectors 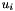 :
:
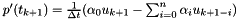
Thus we have
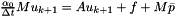
with
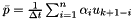
This class stores the n last state vectors in order to be able to calculate 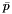 . It also provides
. It also provides 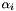 and can extrapolate the the new state from the n last states with a polynomial of order n-1:
and can extrapolate the the new state from the n last states with a polynomial of order n-1:
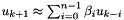
The class allows to change the time-steps, recomputing the coefficients. to change 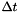 at each time-step, use shift_right(uCurrent, timeStepNew) instead of shift_right(uCurrent).
at each time-step, use shift_right(uCurrent, timeStepNew) instead of shift_right(uCurrent).
Other methods that could be helpful while adapting in time are: set_deltat, store_unk and restore_unk
Definition at line 97 of file TimeAdvanceBDFVariableStep.hpp.
| typedef ScalarVector container_Type |
Definition at line 103 of file TimeAdvanceBDFVariableStep.hpp.
| typedef FEVectorType feVector_Type |
Definition at line 104 of file TimeAdvanceBDFVariableStep.hpp.
| typedef std::shared_ptr< feVector_Type > feVectorPtr_Type |
Definition at line 105 of file TimeAdvanceBDFVariableStep.hpp.
| typedef std::vector< feVectorPtr_Type > feVectorPtrContainer_Type |
Definition at line 106 of file TimeAdvanceBDFVariableStep.hpp.
Empty constructor.
Definition at line 332 of file TimeAdvanceBDFVariableStep.hpp.
Destructor.
Definition at line 342 of file TimeAdvanceBDFVariableStep.hpp.
| void setup | ( | const UInt | order | ) |
Setup the TimeAdvanceBDFVariableStep with order n.
| order | order of the BDF |
Definition at line 349 of file TimeAdvanceBDFVariableStep.hpp.
| void setInitialCondition | ( | feVector_Type | u0, |
| Real const | timeStep, | ||
| bool | startup = 0 |
||
| ) |
Initialize all the entries of the unknown vector to be derived with the vector u0 (duplicated if startup=0)
If startup = 0, it initializes all the entries of the unknown vectors with a given function The array of initial conditions needed by the selected BDF is initialized as follows: unk=[ u0(t0), u0(t0-dt), u0(t0-2*dt), ...] When startUp = true, only M_unknown[0] is initialized (with u0). At the first step, class Bfd computes the coefficients of BDF1, at the second step, the coefficient of BDF2, and so on, until it reaches the wanted method. Second order of accuracy is obtained using this procedure to startup BDF2. Using the startup procedure with BDF3, the accuracy order is limited to the second order; anyway it is better to use the startup procedure instead of taking u{-2} = u_{-1} = u_0.
| u0 | initial condition vector |
| timeStep | time step |
| startup |
Definition at line 370 of file TimeAdvanceBDFVariableStep.hpp.
| void setInitialCondition | ( | std::vector< feVector_Type > | u0s, |
| Real const | timeStep | ||
| ) |
Initialize all the entries of the unknown vector to be derived with a set of vectors u0s.
| u0s | initial condition vectors |
| timeStep | time step |
Definition at line 395 of file TimeAdvanceBDFVariableStep.hpp.
| void setInitialCondition | ( | const FunctionType & | u0Function, |
| feVector_Type & | u0Vector, | ||
| FESpaceType & | feSpace, | ||
| Real | t0, | ||
| Real | timeStep | ||
| ) |
Initialize all the entries of the unknonwn vectors with a given function.
The array of initial conditions needed by the selected BDF is initialized as follows: M_unknown=[ u0Function(t0), u0Function(t0-dt), u0Function(t0-2*dt), ...] For the space dependence of the initial conditions we need informations on:
| u0Function | the function we want to interpolate |
| u0Vector | corrected mapped vector, it contains the u0Function(t0) in output |
| feSpace | finite element space |
| t0 | initial time (t0) and the |
| timeStep | time step (for solutions before the initial instant) |
Based on the NavierStokesHandler::initialize by M. Fernandez
Definition at line 426 of file TimeAdvanceBDFVariableStep.hpp.
| TimeAdvanceBDFVariableStep< FEVectorType >::feVector_Type rhsContribution | ( | ) | const |
Returns the right hand side 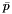 of the time derivative formula divided by dt.
of the time derivative formula divided by dt.
Definition at line 448 of file TimeAdvanceBDFVariableStep.hpp.
| TimeAdvanceBDFVariableStep< FEVectorType >::feVector_Type rhsContributionTimeStep | ( | Real | timeStep = 1 | ) | const |
Returns the right hand side 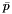 of the time derivative formula divided by timeStep (backward compatibility version, will be discontinued)
of the time derivative formula divided by timeStep (backward compatibility version, will be discontinued)
| timeStep | time step, 1 by default |
Definition at line 464 of file TimeAdvanceBDFVariableStep.hpp.
| TimeAdvanceBDFVariableStep< FEVectorType >::feVector_Type extrapolateSolution | ( | ) | const |
Compute the polynomial extrapolation approximation of order n-1 of u^{n+1} defined by the n stored state vectors.
Definition at line 480 of file TimeAdvanceBDFVariableStep.hpp.
| void shiftRight | ( | feVector_Type const & | uCurrent | ) |
Update the vectors of the previous time steps by shifting on the right the old values.
| uCurrent | current (new) value of the state vector |
Definition at line 496 of file TimeAdvanceBDFVariableStep.hpp.
| void shiftRight | ( | feVector_Type const & | uCurrent, |
| Real | timeStepNew | ||
| ) |
Update the vectors of the previous time steps by shifting on the right the old values.
Set the the new time step and shift right the old time steps.
| uCurrent | current (new) value of the state vector |
| timeStepNew | new value of the time step |
Definition at line 521 of file TimeAdvanceBDFVariableStep.hpp.
| void storeSolution | ( | ) |
Save the current vector M_unknowns and the current vector M_timeStep.
Definition at line 548 of file TimeAdvanceBDFVariableStep.hpp.
| void restoreSolution | ( | ) |
Restore the vector M_unknowns and the vector M_timeStep with the ones saved with store_unk()
Definition at line 563 of file TimeAdvanceBDFVariableStep.hpp.
| void restoreSolution | ( | Real | timeStep | ) |
It is equivalent to do : storeSolution() + setTimeStep()
| timeStep | new time step |
Definition at line 580 of file TimeAdvanceBDFVariableStep.hpp.
| void showMe | ( | ) | const |
Show informations about the BDF.
Definition at line 598 of file TimeAdvanceBDFVariableStep.hpp.
| void setTimeStep | ( | Real | timeStep | ) |
Replace the current time-step with timeStep and computes the coefficients a_i and beta_i as functions of M_timeStep.
| timeStep | time step |
Definition at line 617 of file TimeAdvanceBDFVariableStep.hpp.
Return the i-th coefficient of the time derivative alpha_i.
| i | index of the coefficient |
Definition at line 628 of file TimeAdvanceBDFVariableStep.hpp.
Return the i-th coefficient of the time derivative alpha_i divided by dt.
| i | index of the coefficient |
Definition at line 639 of file TimeAdvanceBDFVariableStep.hpp.
Return the i-th coefficient of the time extrapolation beta_i.
| i | index of the coefficient |
Definition at line 650 of file TimeAdvanceBDFVariableStep.hpp.
|
inline |
Return the vector of the time steps, ordered starting from the most recent one.
Definition at line 261 of file TimeAdvanceBDFVariableStep.hpp.
|
inline |
Return a vector with the last n state vectors.
Definition at line 267 of file TimeAdvanceBDFVariableStep.hpp.
|
inline |
Definition at line 272 of file TimeAdvanceBDFVariableStep.hpp.
|
private |
Private methods.
Computes the coefficients a_i and beta_i as functions of _M_delta_t.
Arbitrary order, variable time step BDF coefficients. Reference: Comincioli pag. 618-619 Matlab implementation: function [alpha0, alpha, beta] = compute_coef(dts, order) assert( (length(dts) == order) ); rho = dts(1)./cumsum(dts);
alpha0 = sum(rho); alpha = zeros(order,1); beta = zeros(order,1);
for j = 1:order ind = setdiff([1:order],j); beta(j) = 1/prod(1-rho(ind)/rho(j)); alpha(j) = rho(j)*beta(j); end
end
Definition at line 662 of file TimeAdvanceBDFVariableStep.hpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
private |
Order of the BDF derivative/extrapolation: the time-derivative coefficients vector has size n+1, the extrapolation vector has size n.
Definition at line 310 of file TimeAdvanceBDFVariableStep.hpp.
|
private |
Coefficients 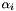 of the time bdf discretization.
of the time bdf discretization.
Definition at line 313 of file TimeAdvanceBDFVariableStep.hpp.
|
private |
Coefficients 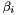 of the extrapolation.
of the extrapolation.
Definition at line 316 of file TimeAdvanceBDFVariableStep.hpp.
|
private |
container_Type 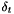 of time intervals
of time intervals
Definition at line 319 of file TimeAdvanceBDFVariableStep.hpp.
|
private |
Definition at line 320 of file TimeAdvanceBDFVariableStep.hpp.
|
private |
Last n state vectors.
Definition at line 323 of file TimeAdvanceBDFVariableStep.hpp.
|
private |
Definition at line 324 of file TimeAdvanceBDFVariableStep.hpp.