 |
LifeV
|
 |
LifeV
|
StabilizationSD Class. More...
#include <StabilizationSD.hpp>
 Collaboration diagram for StabilizationSD< MeshType, DofType >:
Collaboration diagram for StabilizationSD< MeshType, DofType >:| typedef MeshType | mesh_Type |
| typedef DofType | dof_Type |
Constructor and Destructor | |
| StabilizationSD (const GetPot &dataFile, const mesh_Type &mesh, const dof_Type &dof, const ReferenceFE &refFE, const QuadratureRule &quadRule, Real viscosity) | |
| Constructor. More... | |
| virtual | ~StabilizationSD () |
| ~Destructor More... | |
Methods | |
| template<typename MatrixType , typename VectorType > | |
| void | applySUPG (const Real dt, MatrixType &matrix, const VectorType &state) |
| compute the SUPG stabilization terms and add them into the monolithic N.S. matrix More... | |
| template<typename MatrixType , typename VectorType > | |
| void | applySD (const Real dt, MatrixType &matrix, const VectorType &state) |
| compute the SD stabilization terms and add them into the Momentum matrix More... | |
| template<typename VectorType , typename SourceType > | |
| void | applyRHS (const Real dt, VectorType &vector, const VectorType &state, const SourceType &source, const Real &time) |
| compute the SUPG stabilization terms and add them into the right and side More... | |
| void | showMe (std::ostream &output=std::cout) const |
| Display class informations. More... | |
Set Methods | |
| void | setGammaBeta (const Real &gammaBeta) |
Set the stabilization parameter 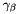 for for 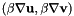 . More... . More... | |
| void | setGammaDiv (const Real &gammaDiv) |
Set the stabilization parameter 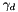 for for 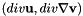 . More... . More... | |
Private Constructor | |
| StabilizationSD () | |
| Default Constructor. More... | |
| StabilizationSD (const StabilizationSD< mesh_Type, dof_Type > &original) | |
| Copy Constructor. More... | |
Private Methods | |
| template<typename VectorType > | |
| void | computeParameters (const Real dt, const UInt iVol, const VectorType &state, VectorElemental &beta, Real &coeffBeta, Real &coeffDiv) const |
| Compute the stabilization coefficients for each element. More... | |
| void | bgradu_bgradv (const Real &coef, VectorElemental &vel, ElemMat &elmat, const CurrentFE &fe, UInt iblock, UInt jblock, UInt nb) const |
Evaluate the varf 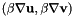 . More... . More... | |
| void | lapu_bgradv (const Real &coef, VectorElemental &vel, MatrixElemental &elmat, const CurrentFE &fe, UInt iblock, UInt jblock, UInt nb) const |
Evaluate the varf 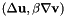 . More... . More... | |
| void | gradp_bgradv (const Real &coef, VectorElemental &vel, MatrixElemental &elmat, const CurrentFE &fe) const |
Evaluate the varf 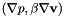 . More... . More... | |
| void | lapu_gradq (const Real &coef, MatrixElemental &elmat, const CurrentFE &fe) const |
Evaluate the varf 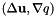 . More... . More... | |
| template<typename SourceType > | |
| void | f_bgradv (const Real &coef, SourceType &source, VectorElemental &vel, VectorElemental &elvec, const CurrentFE &fe, UInt iblock, const Real &time) const |
Evaluate the varf 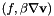 . More... . More... | |
| template<typename SourceType > | |
| void | f_gradq (const Real &coef, SourceType &source, VectorElemental &elvec, const CurrentFE &fe, UInt iblock, const Real &time) const |
Evaluate the varf 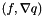 . More... . More... | |
Private Attributes | |
| const mesh_Type & | M_mesh |
| the mesh object More... | |
| const dof_Type & | M_dof |
| the dof object More... | |
| CurrentFE | M_fe |
| current fe for the assembling of stabilization terms. More... | |
| Real | M_viscosity |
fluid viscosity 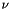 More... More... | |
| Real | M_gammaBeta |
Stabilization coefficient of 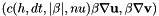 . More... . More... | |
| Real | M_gammaDiv |
Stabilization coefficient of 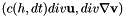 . More... . More... | |
| MatrixElemental | M_elMat |
| Elementary Matrix for assembling the stabilization terms. More... | |
| VectorElemental | M_elVec |
| Elementary Vector for assembling the stabilization terms. More... | |
StabilizationSD Class.
Streamline diffusion and SUPG for Navier-Stokes
Implementation of streamline diffusion (SD) and SUPG for the Navier-Stokes equations.
SUPG can be used only with equal order finite element for the discretization of velocity and pressure fields.
Definition at line 59 of file StabilizationSD.hpp.
Definition at line 65 of file StabilizationSD.hpp.
| typedef DofType dof_Type |
Definition at line 66 of file StabilizationSD.hpp.
| StabilizationSD | ( | const GetPot & | dataFile, |
| const mesh_Type & | mesh, | ||
| const dof_Type & | dof, | ||
| const ReferenceFE & | refFE, | ||
| const QuadratureRule & | quadRule, | ||
| Real | viscosity | ||
| ) |
Constructor.
| dataFile | GetPot dataFile where to read the stabilization parameter |
| mesh | mesh_Type mesh |
| dof | dof_Type velocity field degree of freedom |
| refFE | refFE velocity field reference finite element |
| quadRule | QuadratureRule quadrature rule for the integration of the stabilization variational forms |
| viscosity | viscosity fluid viscosity 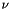 |
Definition at line 236 of file StabilizationSD.hpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinevirtual |
~Destructor
Definition at line 87 of file StabilizationSD.hpp.
|
private |
Default Constructor.
|
private |
Copy Constructor.
| void applySUPG | ( | const Real | dt, |
| MatrixType & | matrix, | ||
| const VectorType & | state | ||
| ) |
compute the SUPG stabilization terms and add them into the monolithic N.S. matrix
This function adds the following stabilization terms to the Navier-Stokes monolithic matrix:
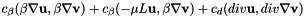
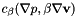
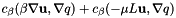
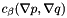
where 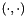 represents the
represents the 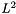 scalar product, and
scalar product, and
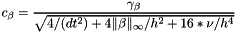 , where
, where 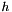 is the diameter of the element;
is the diameter of the element; 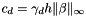 .
. Both high Pechlet numbers and inf-sup incompatible FEM are stabilized.
PREREQUISITE: The velocity and the pressure field should belong to the same finite element space
Parameters are the followings:
| dt | Real timestep (INPUT) |
| matrix | MatrixType where the stabilization terms are added into. (OUTPUT) |
| state | VectorType velocity field for the linearization of the stabilization (INPUT) |
Definition at line 257 of file StabilizationSD.hpp.
| void applySD | ( | const Real | dt, |
| MatrixType & | matrix, | ||
| const VectorType & | state | ||
| ) |
compute the SD stabilization terms and add them into the Momentum matrix
The following stabilization term is added: 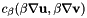
| dt | Real timestep |
| matrix | MatrixType where the stabilization terms are added into |
| state | VectorType velocity field for the linearization of the stabilization |
Definition at line 344 of file StabilizationSD.hpp.
| void applyRHS | ( | const Real | dt, |
| VectorType & | vector, | ||
| const VectorType & | state, | ||
| const SourceType & | source, | ||
| const Real & | time | ||
| ) |
compute the SUPG stabilization terms and add them into the right and side
Add the following stabilization terms to rhs
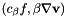 ;
; 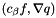 .
. | dt | Real timestep |
| vector | VectorType where the stabilization terms are added into |
| state | VectorType velocity field for the linearization of the stabilization |
| source | SourceType a functor f(time, x, y, z, ic) which represents the forcing term |
| time | REAL the actual time in which source should be evaluated |
Definition at line 417 of file StabilizationSD.hpp.
| void showMe | ( | std::ostream & | output = std::cout | ) | const |
Display class informations.
Definition at line 487 of file StabilizationSD.hpp.
|
inline |
Set the stabilization parameter 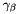 for
for 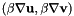 .
.
Definition at line 156 of file StabilizationSD.hpp.
|
inline |
Set the stabilization parameter 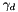 for
for 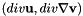 .
.
Definition at line 161 of file StabilizationSD.hpp.
|
private |
Compute the stabilization coefficients for each element.
Definition at line 502 of file StabilizationSD.hpp.
|
private |
Evaluate the varf 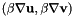 .
.
Definition at line 592 of file StabilizationSD.hpp.
|
private |
Evaluate the varf 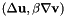 .
.
Definition at line 651 of file StabilizationSD.hpp.
|
private |
Evaluate the varf 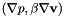 .
.
Definition at line 545 of file StabilizationSD.hpp.
|
private |
Evaluate the varf 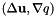 .
.
Definition at line 714 of file StabilizationSD.hpp.
|
private |
Evaluate the varf 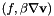 .
.
Definition at line 748 of file StabilizationSD.hpp.
|
private |
Evaluate the varf 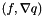 .
.
Definition at line 793 of file StabilizationSD.hpp.
|
private |
the mesh object
Definition at line 213 of file StabilizationSD.hpp.
|
private |
the dof object
Definition at line 215 of file StabilizationSD.hpp.
|
private |
current fe for the assembling of stabilization terms.
Definition at line 217 of file StabilizationSD.hpp.
|
private |
fluid viscosity 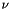
Definition at line 219 of file StabilizationSD.hpp.
|
private |
Stabilization coefficient of 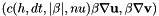 .
.
Definition at line 221 of file StabilizationSD.hpp.
|
private |
Stabilization coefficient of 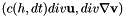 .
.
Definition at line 223 of file StabilizationSD.hpp.
|
private |
Elementary Matrix for assembling the stabilization terms.
Definition at line 225 of file StabilizationSD.hpp.
|
private |
Elementary Vector for assembling the stabilization terms.
Definition at line 227 of file StabilizationSD.hpp.