LifeV
OneDFSIFluxNonLinear Class Reference

OneDFSIFluxNonLinear - Class containing the non-linear flux term 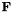$\mathbf F$ of the 1D hyperbolic problem. More...

#include <OneDFSIFluxNonLinear.hpp>

+ Inheritance diagram for OneDFSIFluxNonLinear:
+ Collaboration diagram for OneDFSIFluxNonLinear:

Type definitions and Enumerators

typedef OneDFSIFlux super
 

Constructors & Destructor

 OneDFSIFluxNonLinear ()
 Empty constructor. More...
 
 OneDFSIFluxNonLinear (const physicsPtr_Type physicsPtr)
 Constructor. More...
 
virtual ~OneDFSIFluxNonLinear ()
 Do nothing destructor. More...
 

Methods

Real flux (const Real &A, const Real &Q, const ID &row, const UInt &iNode) const
 Evaluate the flux term. More...
 
Real dFdU (const Real &A, const Real &Q, const ID &row, const ID &column, const UInt &iNode) const
 Evaluate the derivative of the flux term. More...
 
void eigenValuesEigenVectors (const Real &A, const Real &Q, container2D_Type &eigenvalues, container2D_Type &leftEigenvector1, container2D_Type &leftEigenvector2, const UInt &iNode) const
 Eigenvalues and eigenvectors of the Jacobian matrix. More...
 
void deltaEigenValuesEigenVectors (const Real &A, const Real &Q, container2D_Type &deltaEigenvalues, container2D_Type &deltaLeftEigenvector1, container2D_Type &deltaLeftEigenvector2, const UInt &iNode) const
 Derivatives of the eigenvalues and eigenvectors of the derivative of the Jacobian matrix. More...
 

Unimplemented Methods

 OneDFSIFluxNonLinear (const OneDFSIFluxNonLinear &flux)
 
OneDFSIFluxNonLinear & operator= (const OneDFSIFluxNonLinear &flux)
 

Additional Inherited Members

- Public Types inherited from OneDFSIFlux
typedef FactorySingleton< Factory< OneDFSIFlux, OneDFSI::fluxTerm_Type > > factoryFlux_Type
 
typedef OneDFSIPhysics physics_Type
 
typedef std::shared_ptr< physics_Type > physicsPtr_Type
 
typedef OneDFSIData::container2D_Type container2D_Type
 
- Public Member Functions inherited from OneDFSIFlux
 OneDFSIFlux ()
 Empty constructor. More...
 
 OneDFSIFlux (const physicsPtr_Type physicsPtr)
 Constructor. More...
 
virtual ~OneDFSIFlux ()
 Do nothing destructor. More...
 
void setPhysics (const physicsPtr_Type &physicsPtr)
 Set the physics of the problem. More...
 
physicsPtr_Type physics () const
 Get the physics of the problem. More...
 
- Protected Attributes inherited from OneDFSIFlux
physicsPtr_Type M_physicsPtr
 

Detailed Description

OneDFSIFluxNonLinear - Class containing the non-linear flux term 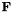$\mathbf F$ of the 1D hyperbolic problem.

Author
Vincent Martin, Cristiano Malossi
See also
Equations and networks of 1-D models [7]
Geometrical multiscale coupling of 1-D models [12] [13] [3]

The conservative form of the generic hyperbolic problem is

\[ \frac{\partial \mathbf U}{\partial t} + \frac{\partial \mathbf F(\mathbf U)}{\partial z} + \mathbf S(\mathbf U) = 0, \]

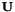where $\mathbf U$ are the conservative variables, 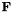$\mathbf F$ the corresponding fluxes, and 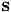$\mathbf S$ represents the source terms.

In the present implementation we have:

\[ \mathbf F(\mathbf U) = \left[\begin{array}{c} Q \\[2ex] \alpha \displaystyle \frac{Q^2}{A} + \displaystyle \displaystyle\int_{0}^A \frac{A}{\rho}\frac{\partial \psi}{\partial A} dA \end{array}\right], \quad \mathbf S(\mathbf U) = \mathbf B(\mathbf U) - \left[\begin{array}{c} 0 \\[2ex] \displaystyle\frac{\partial}{\partial A^0}\displaystyle\int_{0}^A \displaystyle\frac{A}{\rho}\displaystyle\frac{\partial \psi}{\partial A} dA \displaystyle\frac{\partial A^0}{\partial z} + \displaystyle\frac{\partial}{\partial \beta_0}\displaystyle\int_{0}^A \displaystyle\frac{A}{\rho}\displaystyle\frac{\partial \psi}{\partial A} dA \displaystyle\frac{\partial \beta_0}{\partial z} + \displaystyle\frac{\partial}{\partial \beta_1}\displaystyle\int_{0}^A \displaystyle\frac{A}{\rho}\displaystyle\frac{\partial \psi}{\partial A} dA \displaystyle\frac{\partial \beta_1}{\partial z} \end{array}\right] \]

where

\[ \mathbf B(\mathbf U) = \left[\begin{array}{c} 0 \\[2ex] K_r \displaystyle\frac{Q}{A} + \displaystyle\frac{A}{\rho}\left(\displaystyle\frac{\partial \psi}{\partial A^0}\displaystyle\frac{\partial A^0}{\partial z} + \displaystyle\frac{\partial \psi}{\partial \beta_0}\displaystyle\frac{\partial \beta_0}{\partial z} + \displaystyle\frac{\partial \psi}{\partial \beta_1}\displaystyle\frac{\partial \beta_1}{\partial z}\right) + \displaystyle\frac{Q^2}{A}\displaystyle\frac{\partial \alpha}{\partial z} \end{array}\right] \]

The assumed wall-law is

\[ P-P_\mathrm{ext} = \psi(A,A^0,\beta_0, \beta_1, \gamma) = \underbrace{\sqrt{\frac{\pi}{A^0}}\frac{h E}{1-\nu^2}}_{\beta_0} \left(\left(\frac{A}{A^0}\right)^{\beta_1}-1\right) + \underbrace{\frac{T \tan\phi}{4 \sqrt{\pi}}\frac{h E}{1-\nu^2}}_{\displaystyle\gamma} \frac{1}{A\sqrt{A}} \frac{\partial A}{\partial t}. \]

This class implements all the interfaces required for the computation of 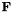$\mathbf F$ and its derivatives.

Definition at line 108 of file OneDFSIFluxNonLinear.hpp.

Member Typedef Documentation

◆ super

typedef OneDFSIFlux super

Definition at line 116 of file OneDFSIFluxNonLinear.hpp.

Constructor & Destructor Documentation

◆ OneDFSIFluxNonLinear() [1/3]

OneDFSIFluxNonLinear ( )
inlineexplicit

Empty constructor.

Definition at line 125 of file OneDFSIFluxNonLinear.hpp.

+ Here is the caller graph for this function:

◆ OneDFSIFluxNonLinear() [2/3]

OneDFSIFluxNonLinear ( const physicsPtr_Type  physicsPtr)
inlineexplicit

Constructor.

Parameters
physicsPtrpointer to the physics of the problem

Definition at line 131 of file OneDFSIFluxNonLinear.hpp.

◆ ~OneDFSIFluxNonLinear()

virtual ~OneDFSIFluxNonLinear ( )
inlinevirtual

Do nothing destructor.

Definition at line 134 of file OneDFSIFluxNonLinear.hpp.

◆ OneDFSIFluxNonLinear() [3/3]

OneDFSIFluxNonLinear ( const OneDFSIFluxNonLinear &  flux)
explicitprivate

Member Function Documentation

◆ flux()

Real flux ( const Real &  A,
const Real &  Q,
const ID &  row,
const UInt &  iNode 
) const
virtual

Evaluate the flux term.

\[ \mathbf F(\mathbf U) = \left[\begin{array}{c} Q \\[2ex] \alpha \displaystyle \frac{Q^2}{A} + \displaystyle\frac{\beta_0 \beta_1 A^0}{\rho(\beta_1+1)}\left(\displaystyle\frac{A}{A^0}\right)^{\beta_1+1} \end{array}\right] \]

Parameters
Aarea
Qflow rate
rowrow of the flux term
iNodenode of the mesh

Implements OneDFSIFlux.

Definition at line 50 of file OneDFSIFluxNonLinear.cpp.

◆ dFdU()

Real dFdU ( const Real &  A,
const Real &  Q,
const ID &  row,
const ID &  column,
const UInt &  iNode 
) const
virtual

Evaluate the derivative of the flux term.

\[ \displaystyle\frac{\partial \mathbf F}{\partial \mathbf U} = \left[\begin{array}{cc} 0 & 1 \\[2ex] \displaystyle\frac{A}{\rho}\displaystyle\frac{\partial \psi}{\partial A} - \alpha \displaystyle\frac{Q^2}{A^2} & 2 \alpha \displaystyle\frac{Q}{A} \end{array}\right] \]

Parameters
Aarea
Qflow rate
rowrow of the derivative of the flux term
columncolumn of the derivative of the flux term
iNodenode of the mesh

Implements OneDFSIFlux.

Definition at line 73 of file OneDFSIFluxNonLinear.cpp.

◆ eigenValuesEigenVectors()

void eigenValuesEigenVectors ( const Real &  A,
const Real &  Q,
container2D_Type &  eigenvalues,
container2D_Type &  leftEigenvector1,
container2D_Type &  leftEigenvector2,
const UInt &  iNode 
) const
virtual

Eigenvalues and eigenvectors of the Jacobian matrix.

\[ \lambda_{1,2} = \alpha \displaystyle\frac{Q}{A} \pm \sqrt{\alpha (\alpha - 1)\left(\displaystyle\frac{Q}{A}\right)^2+ \displaystyle\frac{A}{\rho}\displaystyle\frac{\partial \psi}{\partial A}}, \]

\[ \displaystyle L = \varsigma \left[\begin{array}{cc} -\lambda_2 & 1\\ -\lambda_1 & 1 \end{array}\right] \]

Parameters
Aarea
Qflow rate
eigenvalueseigenvalues of the Jacobian matrix
leftEigenvector1first row of the left eigenvector matrix
leftEigenvector2second row of the left eigenvector matrix
iNodenode of the mesh

Implements OneDFSIFlux.

Definition at line 105 of file OneDFSIFluxNonLinear.cpp.

◆ deltaEigenValuesEigenVectors()

void deltaEigenValuesEigenVectors ( const Real &  A,
const Real &  Q,
container2D_Type &  deltaEigenvalues,
container2D_Type &  deltaLeftEigenvector1,
container2D_Type &  deltaLeftEigenvector2,
const UInt &  iNode 
) const
virtual

Derivatives of the eigenvalues and eigenvectors of the derivative of the Jacobian matrix.

\[ \begin{array}{@{}r@{}c@{}l} \displaystyle\frac{\partial \lambda_{1,2}}{\partial z} & = & \displaystyle\frac{\partial \lambda_{1,2}}{\partial A^0}\displaystyle\frac{\partial A^0}{\partial z} + \displaystyle\frac{\partial \lambda_{1,2}}{\partial \beta_0}\displaystyle\frac{\partial \beta_0}{\partial z} + \displaystyle\frac{\partial \lambda_{1,2}}{\partial \beta_1}\displaystyle\frac{\partial \beta_1}{\partial z} + \displaystyle\frac{\partial \lambda_{1,2}}{\partial \alpha}\displaystyle\frac{\partial \alpha}{\partial z}\\[4ex] & = & \displaystyle\frac{Q}{A}\displaystyle\frac{\partial \alpha}{\partial z} \pm \displaystyle\frac{1}{2}\left(\alpha (\alpha - 1)\left(\displaystyle\frac{Q}{A}\right)^2+ \displaystyle\frac{A}{\rho}\displaystyle\frac{\partial \psi}{\partial A}\right)^{-1/2}\left(\displaystyle\frac{A}{\rho} \left(\displaystyle\frac{\partial^2 \psi}{\partial A \partial A^0}\displaystyle\frac{\partial A^0}{\partial z} + \displaystyle\frac{\partial^2 \psi}{\partial A \partial \beta_0}\displaystyle\frac{\partial \beta_0}{\partial z} + \displaystyle\frac{\partial^2 \psi}{\partial A \partial \beta_1}\displaystyle\frac{\partial \beta_1}{\partial z}\right) + (2\alpha - 1)\left(\displaystyle\frac{Q}{A}\right)^2 \displaystyle\frac{\partial \alpha}{\partial z}\right). \end{array} \]

\[ \displaystyle\frac{\partial L}{\partial z} = \varsigma \left[\begin{array}{cc} -\displaystyle\frac{\partial \lambda_2}{\partial z} & 0\\[4ex] -\displaystyle\frac{\partial \lambda_1}{\partial z} & 0 \end{array}\right] \]

Parameters
Aarea
Qflow rate
deltaEigenvaluesderivative of the eigenvalues of the derivative of the Jacobian matrix
deltaLeftEigenvector1derivative of the first row of the left eigenvector matrix
deltaLeftEigenvector2derivative of the second row of the left eigenvector matrix
iNodenode of the mesh

Implements OneDFSIFlux.

Definition at line 134 of file OneDFSIFluxNonLinear.cpp.

◆ operator=()

OneDFSIFluxNonLinear& operator= ( const OneDFSIFluxNonLinear &  flux)
private
The documentation for this class was generated from the following files: