 |
LifeV
|
 |
LifeV
|
GodunovNumericalFlux Gives an implementation for Godunov solver for hyperbolic's flux function. More...
#include <HyperbolicFluxNumerical.hpp>
 Inheritance diagram for GodunovNumericalFlux< Mesh, SolverType >:
Inheritance diagram for GodunovNumericalFlux< Mesh, SolverType >: Collaboration diagram for GodunovNumericalFlux< Mesh, SolverType >:
Collaboration diagram for GodunovNumericalFlux< Mesh, SolverType >:Protected Attributes | |
| Real | M_brentToll |
| Tollerance for the Brent algorithm used for Godunov flux. More... | |
| UInt | M_brentMaxIter |
| Maximum of iteration for the Brent algorithm used for Godunov flux. More... | |
 Protected Attributes inherited from AbstractNumericalFlux< Mesh, SolverType > Protected Attributes inherited from AbstractNumericalFlux< Mesh, SolverType > | |
| vectorFunction_Type | M_physicalFlux |
| Physical flux function. More... | |
| vectorFunction_Type | M_firstDerivativePhysicalFlux |
| First derivative, respect to unknown, of physical flux function. More... | |
| Real | M_CFLBrentToll |
| Tollerance for the Brent algorithm for computing the CFL condition. More... | |
| UInt | M_CFLBrentMaxIter |
| Maximum of iterations for the Brent algorithm for computing the CFL condition. More... | |
| const FESpace< Mesh, MapEpetra > & | M_fESpace |
| Finite element space of the hyperbolic solver. More... | |
| std::vector< const vectorPtr_Type *> | M_fields |
| Vector of pointers for the dependences of the permeability to external vector fields. More... | |
Public Types | |
| typedef AbstractNumericalFlux< Mesh, SolverType >::vectorFunction_Type | vectorFunction_Type |
| typedef AbstractNumericalFlux< Mesh, SolverType >::scalarFunction_Type | scalarFunction_Type |
| typedef AbstractNumericalFlux< Mesh, SolverType >::dataFile_Type | dataFile_Type |
| typedef AbstractNumericalFlux< Mesh, SolverType >::normal_Type | normal_Type |
Constructors and destructor | |
| GodunovNumericalFlux (const vectorFunction_Type &physicalFlux, const vectorFunction_Type &firstDerivativePhysicalFlux, const FESpace< Mesh, MapEpetra > &fESpace, const dataFile_Type &data, const std::string §ion="numerical_flux/") | |
| Constructor for the class. More... | |
| virtual | ~GodunovNumericalFlux () |
| Virtual destructor. More... | |
Operators | |
| virtual Real | operator() (const Real &leftState, const Real &rightState, const normal_Type &normal, const UInt &iElem, const Real &t=0, const Real &x=0, const Real &y=0, const Real &z=0) const |
| Computes the face contribution of the flux. More... | |
Additional Inherited Members | |
 Public Types inherited from AbstractNumericalFlux< Mesh, SolverType > Public Types inherited from AbstractNumericalFlux< Mesh, SolverType > | |
| typedef std::function< Vector(const Real &, const Real &, const Real &, const Real &, const std::vector< Real > &) > | vectorFunction_Type |
| typedef std::function< Real(const Real &) > | scalarFunction_Type |
| typedef SolverType::vector_type | vector_Type |
| typedef std::shared_ptr< vector_Type > | vectorPtr_Type |
| typedef GetPot | dataFile_Type |
| typedef KN< Real > | normal_Type |
 Public Member Functions inherited from AbstractNumericalFlux< Mesh, SolverType > Public Member Functions inherited from AbstractNumericalFlux< Mesh, SolverType > | |
| AbstractNumericalFlux (const vectorFunction_Type &physicalFlux, const vectorFunction_Type &firstDerivativePhysicalFlux, const FESpace< Mesh, MapEpetra > &fESpace, const dataFile_Type &data, const std::string §ion="numerical_flux/") | |
| Constructor for the class. More... | |
| virtual | ~AbstractNumericalFlux () |
| Virtual destructor. More... | |
| void | setExternalField (const vectorPtr_Type &field) |
| Add one external field. More... | |
| vectorFunction_Type | physicalFlux () const |
| Return the physical flux. More... | |
| vectorFunction_Type | firstDerivativePhysicalFlux () const |
| Return the first derivative, respect to the unknown, of the physical flux. More... | |
| Real | physicalFluxDotNormal (const normal_Type &normal, const UInt &iElem, const Real &t, const Real &x, const Real &y, const Real &z, const Real &unknown) const |
| Evaluate the flux dot normal in a given point of a face. More... | |
| Real | firstDerivativePhysicalFluxDotNormal (const normal_Type &normal, const UInt &iElem, const Real &t, const Real &x, const Real &y, const Real &z, const Real &unknown) const |
| Evaluate the first derivative of the flux dot normal in a given point of a face. More... | |
| Real | normInfinity (const Real &leftState, const Real &rightState, const normal_Type &normal, const UInt &iElem, const Real &t=0, const Real &x=0, const Real &y=0, const Real &z=0) const |
| Computes the local infinity norm of the first derivative of the flux dot normal. More... | |
 Protected Member Functions inherited from AbstractNumericalFlux< Mesh, SolverType > Protected Member Functions inherited from AbstractNumericalFlux< Mesh, SolverType > | |
| scalarFunction_Type | computeFunctionDotNormal (const vectorFunction_Type &function, const normal_Type &normal, const UInt &iElem, const Real &t, const Real &x, const Real &y, const Real &z, const Real &plusMinus) const |
| Return a scalar function from a general vector function dot normal in a given point of a face. More... | |
| scalarFunction_Type | computeAbsFunctionDotNormal (const vectorFunction_Type &function, const normal_Type &normal, const UInt &iElem, const Real &t, const Real &x, const Real &y, const Real &z, const Real &plusMinus) const |
| Return a scalar function from the absolute value of a general vector function dot normal in a given point of a face. More... | |
GodunovNumericalFlux Gives an implementation for Godunov solver for hyperbolic's flux function.
This class gives an implementation for Godunov solver for hyperbolic's flux functions 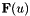 . In particular it implements
. In particular it implements
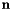 ;
; 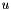 , dot product the outward unit normal;
, dot product the outward unit normal; 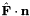 between to adjacent elements computed using Godunov solver
between to adjacent elements computed using Godunov solver
![\[ \hat{\mathbf{F}} \cdot \mathbf{n} (a,b)= \left\{ \begin{array}{l l} \displaystyle \min_{a \leq u \leq b} \mathbf{F} \cdot \mathbf{n} ( u ) & \mathrm{if} \quad a \leq b\,, \\ \displaystyle \max_{b \leq u \leq a} \mathbf{F} \cdot \mathbf{n} ( u ) & \mathrm{otherwise}\,. \end{array} \right. \]](form_102.png)
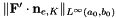 between to adjacent elements.
between to adjacent elements. The class can handle the dependeces of the flux function 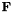 of external vector or scalar fields.
of external vector or scalar fields.
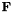 we suppose that the first parameter of the vector is the unknown. See the test case for an example.
we suppose that the first parameter of the vector is the unknown. See the test case for an example. Definition at line 527 of file HyperbolicFluxNumerical.hpp.
| typedef AbstractNumericalFlux<Mesh, SolverType>::vectorFunction_Type vectorFunction_Type |
Definition at line 535 of file HyperbolicFluxNumerical.hpp.
| typedef AbstractNumericalFlux<Mesh, SolverType>::scalarFunction_Type scalarFunction_Type |
Definition at line 536 of file HyperbolicFluxNumerical.hpp.
| typedef AbstractNumericalFlux<Mesh, SolverType>::dataFile_Type dataFile_Type |
Definition at line 537 of file HyperbolicFluxNumerical.hpp.
| typedef AbstractNumericalFlux<Mesh, SolverType>::normal_Type normal_Type |
Definition at line 538 of file HyperbolicFluxNumerical.hpp.
| GodunovNumericalFlux | ( | const vectorFunction_Type & | physicalFlux, |
| const vectorFunction_Type & | firstDerivativePhysicalFlux, | ||
| const FESpace< Mesh, MapEpetra > & | fESpace, | ||
| const dataFile_Type & | data, | ||
| const std::string & | section = "numerical_flux/" |
||
| ) |
Constructor for the class.
| physicalFlux | Physical flux for the problem. |
| firstDerivativePhysicalFlux | First derivative, respect the the unknown, of the physical flux. |
| fESpace | Finite element space of the hyperbolic problem. |
| data | Data for the problem. |
| section | Section for read the data from GetPot file. |
Definition at line 614 of file HyperbolicFluxNumerical.hpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
virtual |
Virtual destructor.
Definition at line 633 of file HyperbolicFluxNumerical.hpp.
|
virtual |
Computes the face contribution of the flux.
Given a face 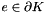 it evaluates
it evaluates
![\[ \max \hat{\mathbf{F}} \cdot \mathbf{n} \]](form_104.png)
between to elements sharing the face, using Godunov flux.
| leftState | Left value of the unknown respect to the face. |
| rightValue | Right value of the unknown respect to the face. |
| normal | Normal of the face. |
| iElem | The ID of the current element in the mesh. |
| t | Current time. |
| x | Abscissa. |
| y | Ordinate. |
| z | Quota. |
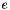 is given by: the normal direction goes from the left side to the right side.
is given by: the normal direction goes from the left side to the right side. Implements AbstractNumericalFlux< Mesh, SolverType >.
Definition at line 645 of file HyperbolicFluxNumerical.hpp.
|
protected |
Tollerance for the Brent algorithm used for Godunov flux.
Definition at line 600 of file HyperbolicFluxNumerical.hpp.
|
protected |
Maximum of iteration for the Brent algorithm used for Godunov flux.
Definition at line 603 of file HyperbolicFluxNumerical.hpp.