ADRAssemblerIP - This class is used to add IP stabilization to an Advection-Diffusion-Reaction problem. More...

#include <ADRAssemblerIP.hpp>

Collaboration diagram for ADRAssemblerIP< mesh_type, matrix_type, vector_type >:

Private Types
typedef MatrixElemental	localMatrix_type

typedef std::unique_ptr< localMatrix_type >	localMatrix_ptrType

typedef CurrentFE	currentFE_type

typedef std::unique_ptr< currentFE_type >	currentFE_ptrType

typedef CurrentFEManifold	currentBdFE_type

typedef std::unique_ptr< currentBdFE_type >	currentBdFE_ptrType

Public Types
typedef MapEpetra	map_Type

typedef FESpace< mesh_type, map_Type >	fespace_type

typedef std::shared_ptr< fespace_type >	fespace_ptrType

typedef std::shared_ptr< matrix_type >	matrix_ptrType

Constructor & Destructor
	ADRAssemblerIP ()
	Empty Constructor. More...

	~ADRAssemblerIP ()
	Destructor. More...

Methods
void	setup (const fespace_ptrType &fespace, const fespace_ptrType &betaFEspace)
	Setup method for the FESpaces. More...

void	addIPStabilizationStencil (const matrix_ptrType &matrixGalerkin, const matrix_ptrType &matrixExtended, const vector_type &beta, const Real &coef)
	This method adds the IP stabilization terms into two matrices depending on the stencil. More...

void	addIPStabilizationStencil (const matrix_ptrType &matrixGalerkin, const matrix_ptrType &matrixExtended, const Real &coef)
	This method adds the IP stabilization on the two matrices, depening on the stencil. More...

void	addIPStabilization (const matrix_ptrType &matrix, const vector_type &beta, const Real &coef)
	This method builds the IP stabilization on a unique matrix (both stencils) More...

void	addIPStabilization (const matrix_ptrType &matrix, const Real &coef)
	Simplest method to add IP stabilization on the matrix. More...

Detailed Description

template<typename mesh_type, typename matrix_type, typename vector_type>
class LifeV::ADRAssemblerIP< mesh_type, matrix_type, vector_type >

ADRAssemblerIP - This class is used to add IP stabilization to an Advection-Diffusion-Reaction problem.

Scope

This is class has been designed to add the IP stabilization for the ADR problem (see in the ADRAssembler class for more detail about that problem). IP stands for Interior Penalty. Indeed, the idea of this stabililization is to penalize the solutions that would exhibit oscillations. To quantify the smoothness of the solution, one can rely on the computation of the jump of gradient across the faces:

$\sum_K \sum_{F \subset K} \int_F [\![ \nabla u ]\!] [\![ \nabla v ]\!]$

where K represents an element and F one of its faces. The IP stabilization consists then in adding the new bilinear form

$\sum_K \sum_{F \subset K} \int_F k [\![ \nabla u ]\!] [\![ \nabla v ]\!]$

in the formulation of the ADR problem to force the solution to be smooth. The coefficient 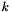$ k $ is used to control the strength of the penalization as well as the good convergence behaviour of the stabilized scheme.

In this class, two choices are possible for 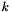$ k $

Usually, the choice is 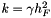$k = \gamma h_F^2$ to ensure the near-optimal convergence of the scheme, 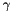$\gamma$ being a fixed parameter.
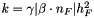For advection dominated flows, it might be easier to use the formula $k = \gamma |\beta \cdot n_F| h_F^2$ . The choice for a suitable constant 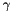$\gamma$ does not depend then on the magnitude of the field 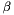$\beta$ and the penalization is somehow better balanced in the domain.

Stencil problems

One of the issues of the IP stabilization is the enlargement of the stencil with respect to the standard Galerkin approximation. Indeed, the IP stabilization couples that would not be coupled otherwise: if we consider a given face F, all the degrees of freedom of the two adjacent elements are coupled together, including degrees of freedom that do not belong to a common element.

From the computational point of view, this can sometimes be not acceptable: the enlarged stencil increases the size of the matrix and (often) the size of the preconditioner (and so the time to compute it). For example, if the LU factorization of matrix is computed, the factors will have much more non-zero entries because the new entries in the matrix are usually "far" from the diagonal.

To eleviate this problem in some situation, this class provides the possibility to assemble the stabilization in two different matrices:

In one of the matrices (matrixGalerkin), the terms concerning basis functions that belong to the same element are added
In the other matrice (matrixExtended), the terms concerning basis functions that do not belong to the same element are added.

This allows to use the first matrix in the system and try to explicit the term corresponding to the second matrix (putting it in the right hand side). For example, when dealing with parabolic ADR problems, one can use the solution of the previous time step (or an extrapolation of the solution) to explicit the stabilization by adding in the right hand side the product of the extended matrix with the approximated solution.

Use

There are two main kind of method: setup methods and stabilization assembly methods.

The setup method is used to simply build the few internal data structures that are needed for the assembly. One should always start by setting up the FESpaces needed.

Once this is done, the assembly can be performed. There are here 4 methods, distinguished by 2 options.

The first option is whether the scaling of the stabilization should depend on the advection field. If one wants to have a scaling 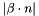$|\beta \cdot n|$ in front of the stabilization, then has to appear in the arguments of the function.

The second option (more advanced) is whether all the terms of the stabilization have to be added to the same matrix. If one want to handle the stencil problem, then two distinct matrices have to be passed to the methods.

Author: Samuel Quinodoz

Remarks: : no choice for the quadrature here, because of currentBDFE.

Definition at line 139 of file ADRAssemblerIP.hpp.

Member Typedef Documentation

◆ map_Type

typedef MapEpetra map_Type

Definition at line 146 of file ADRAssemblerIP.hpp.

◆ fespace_type

typedef FESpace<mesh_type, map_Type> fespace_type

Definition at line 148 of file ADRAssemblerIP.hpp.

◆ fespace_ptrType

typedef std::shared_ptr<fespace_type> fespace_ptrType

Definition at line 149 of file ADRAssemblerIP.hpp.

◆ matrix_ptrType

typedef std::shared_ptr<matrix_type> matrix_ptrType

Definition at line 151 of file ADRAssemblerIP.hpp.

◆ localMatrix_type

typedef MatrixElemental localMatrix_type

private

Definition at line 223 of file ADRAssemblerIP.hpp.

◆ localMatrix_ptrType

typedef std::unique_ptr<localMatrix_type> localMatrix_ptrType

private

Definition at line 224 of file ADRAssemblerIP.hpp.

◆ currentFE_type

typedef CurrentFE currentFE_type

private

Definition at line 226 of file ADRAssemblerIP.hpp.

◆ currentFE_ptrType

typedef std::unique_ptr<currentFE_type> currentFE_ptrType

private

Definition at line 227 of file ADRAssemblerIP.hpp.

◆ currentBdFE_type

typedef CurrentFEManifold currentBdFE_type

private

Definition at line 229 of file ADRAssemblerIP.hpp.

◆ currentBdFE_ptrType

typedef std::unique_ptr<currentBdFE_type> currentBdFE_ptrType

private

Definition at line 230 of file ADRAssemblerIP.hpp.

Constructor & Destructor Documentation

◆ ADRAssemblerIP()

ADRAssemblerIP ( )

Empty Constructor.

Definition at line 264 of file ADRAssemblerIP.hpp.

◆ ~ADRAssemblerIP()

~ADRAssemblerIP ( )

inline

Destructor.

Definition at line 163 of file ADRAssemblerIP.hpp.

Member Function Documentation

◆ setup()

void setup	(	const fespace_ptrType &	fespace,
		const fespace_ptrType &	betaFEspace
	)

Setup method for the FESpaces.

Definition at line 292 of file ADRAssemblerIP.hpp.

◆ addIPStabilizationStencil() [1/2]

void addIPStabilizationStencil	(	const matrix_ptrType &	matrixGalerkin,
		const matrix_ptrType &	matrixExtended,
		const vector_type &	beta,
		const Real &	coef
	)

This method adds the IP stabilization terms into two matrices depending on the stencil.

This method is the main method of this class. It adds the IP stabilization terms into two matrices, matrixGalerkin and matrixExtended. In the matrix Galerkin, the terms for the terms of the Galerkin stencil are added. In the matrix Extended, the terms for the eventually extra stencil are added. Beta is the transport field (given for the betaFESpace), coef is a coefficient that is put in front of all the terms.

Definition at line 327 of file ADRAssemblerIP.hpp.

◆ addIPStabilizationStencil() [2/2]

void addIPStabilizationStencil	(	const matrix_ptrType &	matrixGalerkin,
		const matrix_ptrType &	matrixExtended,
		const Real &	coef
	)

This method adds the IP stabilization on the two matrices, depening on the stencil.

However, it does not take into account the advection field to balance the stabilization.

Definition at line 562 of file ADRAssemblerIP.hpp.

◆ addIPStabilization() [1/2]

void addIPStabilization	(	const matrix_ptrType &	matrix,
		const vector_type &	beta,
		const Real &	coef
	)

inline

This method builds the IP stabilization on a unique matrix (both stencils)

This method takes also into account the transport field for wieghting the stabilization.

Definition at line 201 of file ADRAssemblerIP.hpp.

◆ addIPStabilization() [2/2]

void addIPStabilization	(	const matrix_ptrType &	matrix,
		const Real &	coef
	)

inline

Simplest method to add IP stabilization on the matrix.

Terms for both stencils are added on the same matrix and the coefficient acts uniformly on the domain (no scaling with the transport field)

Definition at line 213 of file ADRAssemblerIP.hpp.

Field Documentation

◆ M_fespace

fespace_ptrType M_fespace

private

Definition at line 234 of file ADRAssemblerIP.hpp.

◆ M_betaFESpace

fespace_ptrType M_betaFESpace

private

Definition at line 237 of file ADRAssemblerIP.hpp.

◆ M_IPFaceCFE

currentBdFE_ptrType M_IPFaceCFE

private

Definition at line 239 of file ADRAssemblerIP.hpp.

◆ M_IPQuad1CFE

currentFE_ptrType M_IPQuad1CFE

private

Definition at line 241 of file ADRAssemblerIP.hpp.

◆ M_IPQuad2CFE

currentFE_ptrType M_IPQuad2CFE

private

Definition at line 242 of file ADRAssemblerIP.hpp.

◆ M_IP1CFE

currentFE_ptrType M_IP1CFE

private

Definition at line 244 of file ADRAssemblerIP.hpp.

◆ M_IP2CFE

currentFE_ptrType M_IP2CFE

private

Definition at line 245 of file ADRAssemblerIP.hpp.

◆ M_IPBetaCFE

currentFE_ptrType M_IPBetaCFE

private

Definition at line 247 of file ADRAssemblerIP.hpp.

◆ M_localIPGalerkin_11

localMatrix_ptrType M_localIPGalerkin_11

private

Definition at line 250 of file ADRAssemblerIP.hpp.

◆ M_localIPGalerkin_22

localMatrix_ptrType M_localIPGalerkin_22

private

Definition at line 251 of file ADRAssemblerIP.hpp.

◆ M_localIPExtended_12

localMatrix_ptrType M_localIPExtended_12

private

Definition at line 254 of file ADRAssemblerIP.hpp.

◆ M_localIPExtended_21

localMatrix_ptrType M_localIPExtended_21

private

Definition at line 255 of file ADRAssemblerIP.hpp.

The documentation for this class was generated from the following file:

ADRAssemblerIP.hpp

Private Attributes
fespace_ptrType	M_fespace

fespace_ptrType	M_betaFESpace

currentBdFE_ptrType	M_IPFaceCFE

currentFE_ptrType	M_IPQuad1CFE

currentFE_ptrType	M_IPQuad2CFE

currentFE_ptrType	M_IP1CFE

currentFE_ptrType	M_IP2CFE

currentFE_ptrType	M_IPBetaCFE

localMatrix_ptrType	M_localIPGalerkin_11

localMatrix_ptrType	M_localIPGalerkin_22

localMatrix_ptrType	M_localIPExtended_12

localMatrix_ptrType	M_localIPExtended_21

Private Types

Private Attributes

Public Types

Constructor & Destructor

Methods

Detailed Description

template<typename mesh_type, typename matrix_type, typename vector_type> class LifeV::ADRAssemblerIP< mesh_type, matrix_type, vector_type >

Member Typedef Documentation

◆ map_Type

◆ fespace_type

◆ fespace_ptrType

◆ matrix_ptrType

◆ localMatrix_type

◆ localMatrix_ptrType

◆ currentFE_type

◆ currentFE_ptrType

◆ currentBdFE_type

◆ currentBdFE_ptrType

Constructor & Destructor Documentation

◆ ADRAssemblerIP()

◆ ~ADRAssemblerIP()

Member Function Documentation

◆ setup()

◆ addIPStabilizationStencil() [1/2]

◆ addIPStabilizationStencil() [2/2]

◆ addIPStabilization() [1/2]

◆ addIPStabilization() [2/2]

Field Documentation

◆ M_fespace

◆ M_betaFESpace

◆ M_IPFaceCFE

◆ M_IPQuad1CFE

◆ M_IPQuad2CFE

◆ M_IP1CFE

◆ M_IP2CFE

◆ M_IPBetaCFE

◆ M_localIPGalerkin_11

◆ M_localIPGalerkin_22

◆ M_localIPExtended_12

◆ M_localIPExtended_21

template<typename mesh_type, typename matrix_type, typename vector_type>
class LifeV::ADRAssemblerIP< mesh_type, matrix_type, vector_type >